zERC20 : Cross-Chain Private ERC-20 Based on ZK Proof-of-Burn

,
1

Review support: INTMAX team

Abstract

Privacy on Ethereum is increasingly important. Yet many existing privacy solutions require extra setup or rely on dedicated wallets and custom UIs.

zERC20 is a privacy-preserving ERC-20 token that integrates zk-Wormhole’s proof-of-burn mechanism. It works seamlessly with standard Web3 wallets, enabling private transfers through the familiar ERC-20 interface.

By using Nova IVC to build the off-chain transfer Merkle tree and to support batch withdrawals, zERC20 achieves lightweight ZK proofs and low on-chain gas costs. In addition, zERC20 natively supports cross-chain private transfers.

Transfer Flow

zERC20 is based on the concept proposed in EIP-7503: Zero-Knowledge Wormholes / Private Proof-of-Burn.

https://ethereum-magicians.org/t/eip-7503-zero-knowledge-wormholes-private-proof-of-burn-ppob/15456

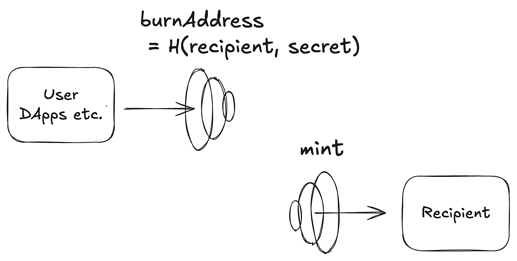
When user A sends tokens to user B, A generates a random secret and computes:

burnAddress = trim160(poseidon(recipient, secret))

A then sends zERC20 tokens to this burnAddress. Because the collision probability is extremely small, the transferred tokens can be regarded as burned.
If B generates this burnAddress and shares it with A, B can hide their actual address.

When B withdraws, they submit a zero-knowledge proof to the Verifier contract proving that:

  1. a zERC20 transfer was made to the corresponding burnAddress; and
  2. they know the secret used to form that burnAddress.

The Verifier mints the same amount of zERC20 tokens to B. To prevent double withdrawals, the contract tracks the cumulative withdrawn amount per destination and only allows minting the difference between received and already withdrawn.

Why Apply zk-Wormholes (EIP-7503) to ERC-20?

The original zk-Wormhole proposal targeted ETH. Since ETH transfers to regular addresses and to burn addresses are indistinguishable at the protocol level, it provides very strong privacy.

By contrast, zERC20 is an ERC-20 token. Transfers to unused addresses can sometimes be distinguished from ordinary transfers. However, as account abstraction (AA) adoption grows, this gap is expected to narrow.

Even so, applying zk-Wormholes to ERC-20 offers several advantages:

  • Wallet compatibility: Private transfers from ordinary wallets via the standard ERC-20 flow.
  • Easy dApp integration: Naturally handled by existing DEXes, lending protocols, and bridges.
  • Cross-chain support: Leverages the zk-Wormhole design to move funds privately across multiple chains.

In short, zERC20 functions similarly to Tornado Cash, but differs in that no special deposit function or UI is required—private transactions are possible using only standard ERC-20 transfer operations.

zk-wormhole
zk-wormhole1316×664 76.6 KB

Technical Details

Notation

  • Fr: the scalar field of bn254.
  • poseidon(a, b): Fr × Fr -> Fr denotes the 2-in-1-out Poseidon hash.
  • A Merkle proof is the list of siblings in a Poseidon-hash binary Merkle tree. merkle_proof.get_root(i, leaf_hash) means computing the Merkle root from the i-th leaf_hash using the proof.
  • trimN trims the lower N bits.

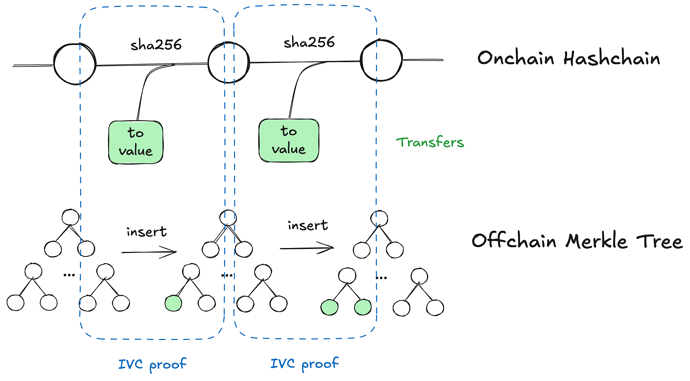
Reducing On-Chain Gas via Off-Chain Merkle Tree Construction

The withdrawal ZKP must prove a transfer to a given burn address. A Merkle proof over a Poseidon-hash tree is efficient for this. However, updating a Merkle tree on-chain (as in Tornado Cash) is expensive (~900k gas), which is unacceptable if we update on every transfer like zERC20.

Therefore, on-chain we use a gas-efficient commitment (a hash chain) and reconstruct an off-chain Merkle tree using Poseidon. This simultaneously lowers on-chain gas and the ZKP cost at withdrawal.

Root Transition Step Circuit

Public input:
[prev_index, prev_hash_chain, prev_transfer_root]

Witness:

  • to ∈ Fr: the 160-bit Ethereum address embedded in Fr.
  • value ∈ Fr: assumed to fit within 248 bits.
  • merkle_proof: the Merkle proof for the prev_index-th element of the transfer tree.

Constraints

  1. new_hash_chain ← trim246(sha256(prev_hash_chain || to || value))
  2. prev_transfer_root == merkle_proof.get_root(prev_index, poseidon(0, 0))
  3. new_transfer_root ← merkle_proof.get_root(prev_index, poseidon(to, value))
  4. new_index ← prev_index + 1

Public output:
[new_index, new_hash_chain, new_transfer_root]

We iteratively apply this step circuit using Nova IVC, producing a transition proof from
[initial_index, initial_hash_chain, initial_transfer_root] to
[current_index, current_hash_chain, current_transfer_root].
We call this the Root Transition Nova.

The Verifier contract queries (index, hashChain) from zERC20 and references them together with the already-proven transferRoot and index as public inputs to the Root Transition Nova. If the proof verifies, it stores newTransferRoot and newIndex. These are later used as public inputs for the withdrawal proof.

transfer
transfer1937×1071 176 KB

Burn Address Generation and Batch Withdrawal

We generate the burn address with Poseidon:

burnAddress = poseidon(recipient, secret)

Here recipient is a generalized recipient computed as:

recipient = trim246(keccak256(recipient_chain_id, recipient_address, tweak))
  • recipient_chain_id: the recipient’s chain id (64 bits)
  • recipient_address: the recipient’s 160-bit address
  • tweak: an arbitrary 32-byte value used to partition the “namespace” of recipient_address (explained below)

We can aggregate multiple withdrawals into one proof with the following circuit. Besides scalability, publishing only the total amount (instead of each individual amount) improves privacy.

Withdraw Step Circuit

Public input:
[transfer_root, prev_index_with_offset, prev_total_value]

Witness:

  • recipient: the recipient bound to the burn address
  • secret: the secret used to generate the burn address
  • value: the amount transferred to the burn address
  • index: the index of that transfer
  • merkle_proof: Merkle proof for index in the transfer tree

Constraints

  1. burn_address ← poseidon(recipient, secret)
  2. Assert transfer_root == merkle_proof.get_root(index, poseidon(burn_address, value))
  3. new_index_with_offset ← index + 1
  4. Assert prev_index_with_offset < new_index_with_offset
  5. new_total_value ← prev_total_value + value

Public output:
[new_index_with_offset, new_total_value]

We iteratively apply this step circuit via Nova, obtaining a Withdraw Nova that transitions from

[transfer_root, recipient, initial_index_with_offset = 0, initial_total_value = 0]
to
[transfer_root, recipient, current_index_with_offset, current_total_value].

By requiring strictly increasing index, we prevent double withdrawals within the same Withdraw Nova proof. The Verifier contract records totalWithdrawn[recipient], the cumulative withdrawn amount per recipient.
Withdrawals proceed as follows:

  1. Receive the components of recipient = trim246(keccak256(recipient_chain_id, recipient_address, tweak)) as arguments and verify that recipient_chain_id == block.chainid.
  2. Verify the Withdraw Nova and ensure proof.recipient matches the recipient from step 1.
  3. Compute delta = proof.current_total_value − totalWithdrawn[recipient] and, only if delta > 0, withdraw (mint) exactly delta.

Notes on burn address and witdrawal

Rotating Recipients via tweak

A Withdraw Nova must process all withdrawals for the same recipient. If there are many receipts, the number of Nova steps can become large. By changing tweak, even for the same (recipient_chain_id, recipient_address) pair, we can change recipient and thus reset the Nova step count.

If you change tweak for every receipt, each withdrawal can be done as a single withdrawal, enabling a lightweight Groth16 proof instead. This is attractive when Nova’s decider proof (a heavier operation that can take ~30 seconds on a MacBook) is undesirable. The trade-off is reduced privacy since single withdrawals reveal the withdrawn amount.

Proof-of-Work for Burn Addresses

If one could find pairs (recipient, secret) and (recipient', secret') such that

trim160(poseidon(recipient, secret)) == trim160(poseidon(recipient', secret'))

then assets sent to that burn address could be withdrawn twice. Due to the birthday paradox, the collision cost is ~80 bits for a 160-bit hash, which is insufficient.
We therefore require a proof-of-work condition: bits 161 through 160 + n of poseidon(recipient, secret) must be zero. This adds n bits of work per attempt, effectively increasing security by n bits.

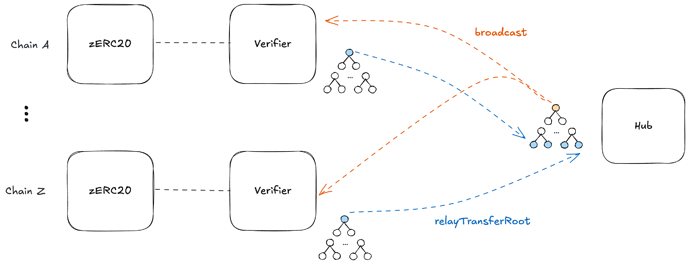
Cross-Chain Transfers

Verifier contracts on each chain transmit their local transfer tree roots to a Hub contract via a cross-chain messaging protocol (e.g., LayerZero). The Hub contract builds a global Merkle tree from these roots and relays the resulting global transfer root back to each chain.

To prevent duplication, the Hub contract must enforce that each chain’s transfer tree is incorporated exactly once into the global tree. With this guarantee, the index within the global tree can serve as the index in the Withdraw Nova proof, preventing double withdrawals. Treating the global transfer tree as a local transfer tree during withdrawals then enables cross-chain burn-and-mint.

global_tree
global_tree2591×998 164 KB

Demo & Implementation

:link: Demo: https://zerc20-demo.vercel.app/
:link: Code: https://github.com/kbizikav/zERC20
The IVC uses Sonobe by PSE.

Gas Costs & ZKP Benchmarks

(ZKP measured on a MacBook Pro with an M4 chip)

Operation Gas / Time
zERC20 transfer 47,834 gas (standard ERC-20 transfer: ~35,016 gas)
Batch withdrawal contract execution 913,922 gas
Single withdrawal contract execution 302,033 gas
Single withdrawal proof generation ~105 ms
Root transition IVC step ~242 ms / step
Root transition decider generation ~32.0 s
Batch withdrawal IVC step ~142 ms / step
Batch withdrawal decider generation ~30.1 s

Related Works

Tornado cash
EIP-7503: zk-Wormholes
EIP-1724: zkERC20
erc721-extension-for-zk-snarks(stealth address)
My previous work for root transition nova
confidential-wrapped-ethereum
removing-pairing-bulletproofs
ERC8065: ZWToken