EVM384 - Feedback and discussion

[axic]

EVM384 is a proposal to extend the EVM with some primitives for efficient 384-bit arithmetics. This would enable the implementation of some operations on new elliptic curves, such as BLS12-381.

The Ewasm team has released an early proposal in May, and today we are releasing a larger write up with the aim to give a comprehensive explanation, and to show some benchmarks:

EVM384 – Can we do Fast Crypto in EVM? - HackMD

Please leave any feedback here.

[shamatar]

Was a subgroup check included into the benchmarks by the way? Number of ops looks quite close to the numbers from the pairing algorithms papers.

[shamatar]

Also you mention an implementation of the BN254 ops through EVM ops that is as gas-cost efficient as a precompile. Was it before the precompile repricing in 1107/1108 or after? Concrete numbers would be great.

I also remember one of the core devs has mentioned that ‘mulmod’ is underpriced, and if it’s true then this comparison is kind of invalid.

[oniki]

@shamatar

Also you mention an implementation of the BN254 ops through EVM ops that is as gas-cost efficient as a precompile. Was it before the precompile repricing in 1107/1108 or after? Concrete numbers would be great.

Yes, it was gas efficient before 1108. See introduction of Weierstrudel

When EIP-1108 goes live all of this work will immediately become redundant

[gcolvin]

I’ve mentioned elsewhere that I prefer a stack-based interface to a memory-based one, as it seems we’d need to use the stack to get things to and from memory anyway. If stack pressure is a concern I’m inclined to increase the stack size anyway.

[shamatar]

Would an opcode that directly use memory pointer be more efficient then a combination of 2xMLOAD and popping two words from the stack after?

I try to look at the Huff implementation of point multiplication to get a sense of now many swaps/dups have to be made. It may be much worse for operations in extension fields where primitive multiplication is kind of N^2 naive multiplication of two polynomials with coefficients of 384 bits.

[gcolvin]

I’m not familiar enough with the code that is being written - or could be written - with these operators to gauge efficiency at that level.

[axic]

We have published a new update at

EVM384 -- Update on the interface - HackMD

[mratsim]

Posting my comment from the Discord channel: (edited 2 links per user

If jwasinger’s EIP1962 (github/jwasinger/eip1962/tree/f472efd5911f395352594bfee13f9fedf14dce1f) is derived from the same code as https://github/kobigurk/wasm_proof it is missing a significant amount of optimizations.
State of the art pairing on BLS12-381 should be between 0.650ms to 0.9ms on 3.0+GHz CPUs from the past 6 years with either MCL github/herumi/mcl or BLST github/supranational/blst or even Consensys Gurvy github/ConsenSys/gurvy or Kilic’s Go implementation github/kilic/bls12-381

Kilic’s EVMBLS might be worth looking at as well (but BN254 github/kilic/evmbls)

Here is a short review of wasm_proof algorithms: Research zkSNARKS blocker: Benchmark and optimize proof time · Issue #7 · vacp2p/research · GitHub
with items worth 10% to 2200% performance boost that are applicable at a high-level (i.e. no assembly).

So given your base speed of 5.5ms

I’m confident we can get significantly faster than the Rust native code.

[shamatar]

To keep things in one place simple tower structure updates for 1962 would give the following numbers without the subgroup checks, on-curve checks, ABI parsing, etc. and without the turbo-boost (that affects numbers by 30%).

test bench::bls12_381_engine::bench_bls12_381_engine_pair_2                             ... bench:   3,127,921 ns/iter (+/- 22,700)
test bench::bls12_381_engine::bench_bls12_381_engine_pair_4                             ... bench:   4,318,937 ns/iter (+/- 36,437)
test bench::bls12_381_engine::bench_bls12_381_engine_pair_6                             ... bench:   5,489,411 ns/iter (+/- 37,720)

Regarding implementations and potential optimizations:

• it uses empty extra bits in field representation
• fused multiplication and reduction is not used to have simpler implementation (it’s a generic library at the end of the day)
• no addition chain in Miller loop (same - generality). Addition: looks like e.g. BLS12-381 addition chain is of length 72, while naive miller loop is 64 doublings and 6 additions, so it’s not obviously necessary for all of the cases
• Fp6 multiplication is sparse
• Lazy reduction is not used (was not even aware of this optimization actually)

So 1962 implementation can be considered as “kind of convenient tool for playing” but should not be considered as the fastest one in a west.

Assembly alone would provide 40% benefit in speed and most likely would bring it very close to other example above. Extra 10% most likely can be shaved on quite a few allocations inside

[mratsim]

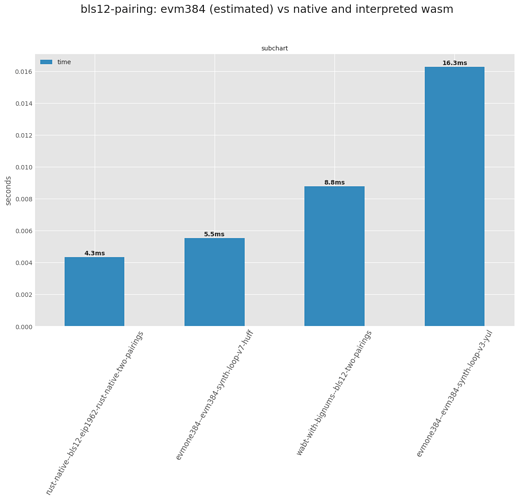
My current benchmarks are:

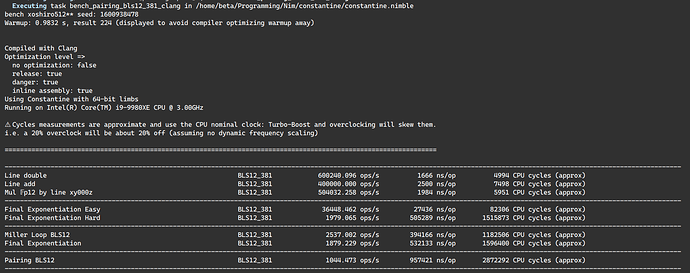
Clang + Assembly

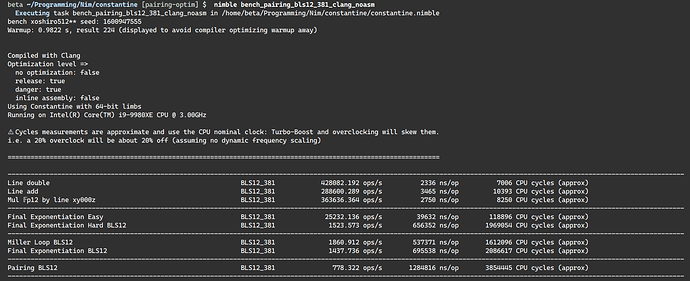
Clang without Assembly (30% slowdown)

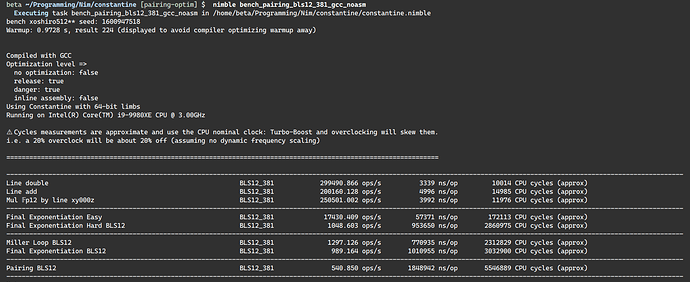
GCC without Assembly (100% slowdown)

CPU has a 3.0GHz nominal clock but is overclocked at 4.1GHz all core turbo and I have a warmup to ensure I’m running at 4.1GHz before bench. You need to scale the time/clock/throughput by 4.1/3 for comparison.

The discrepancy between Clang and GCC in no assembly is because GCC is just bad at bigints.

Note that my numbers are for a single pairing, multi-pairing is not implemented yet. N-way pairing would be N * Miller-loop + 1 final exponentiation.

So using Clang without assembly would take about 1.8ms as it stands with/without the following optimizations:

• no extra bits, use full word bitwidth (which lead to carries which GCC doesn’t properly deal with without assembly)
• no assembly
• CIOS or FIPS multiplication (those are generics to all fields like the separate mul and reduce, called SOS)
• no addition chain in Miller loop
• addition chain in final exponentiation by x
• addition chain for inversion
• Towering is Fp -> Fp2 -> Fp4 -> Fp12 (mostly because I had trouble debugging line functions with Fp6 towering)
• Sparse Fp12 x line multiplication
• no lazy reduction (didn’t work for me, will revisit)
• projective coordinates with constant-time formulae
• no fused line evaluation and elliptic addition/doubling
• mixed addition in Miller loop

BLST on my machine is https://github.com/status-im/nim-blst/issues/1

Pairing (Miller loop + Final Exponentiation)                   1315.289 ops/s       760289 ns/op      2280892 cycles
Pairing (Miller loop + Final Exponentiation) MULX/ADOX/ADCX    1639.054 ops/s       610108 ns/op      1830347 cycles

MCL has a recent PR that fixed inversion and takes a similar amount of time 1.9 Mcycles so about 630 ns/op.

Note: scaling factor between my overclock and the nominal clock.

I expect my biggest contributor to my 20% diff with BLST and MCL is that they are using the Fp6 line evaluation formulas that fused line evaluation and point doubling/addition. They don’t exist in straight line code for Fp4 so I didn’t get to implement them yet (though I’ll likely switch back to Fp6).

So in conclusion from @shamatar’s post and mine I think 2ms double-pairing for native code is a reasonable baseline to compare the EVM against. Also many of those optimizations are generic and portable to the EVM except addition chains which like @shamatar mentions doesn’t save that much for BLS12-381 (a couple thousand cycles out of 2 millions)

Additionally the code for Zexe supports all required curves and has underwent significant optimizations, including assembly code generation and can be use for benchmarks or also as an extra implementation to test against: https://github.com/scipr-lab/zexe/issues/162

[shamatar]

Did anyone try to explore partial Montgomery reduction for BLS12-381? It has enough space at the top of the highest limb, so some additions/subtractions can be made branchless, same for Montgomery multiplication - final reduction can be avoided. I’d suspect around 10-15% here.

[mratsim]

I use it.

Not on my machine but IIRC without assembly I had 136 cycles without and 115 cycles with the optimization.
MCL via LLVM IR has 122 cycles without the optimization.

My basic Montgomery Mul with MULX, ADOX, ADCX + partial reduction is 88 cycles.

AFAIK Geth also uses that optimization since Kilic’s BLS12-381 was merged into Geth and does use it: https://github.com/kilic/bls12-381, https://github.com/ethereum/go-ethereum/pull/21018

BLST and MCL do not use that optimization.

Zexe should use it.

[axic]

We have published a new update at

EVM384 Update 3 - HackMD

Spoiler: A lot of progress has been made on implementing the pairing operation on bls12-381: the miller loop is implemented, but the final exponentation is not yet.

[poemm]

We have published a new update at https://notes.ethereum.org/@poemm/evm384-update4

Spoiler: BLS12-381 pairings implementation is done.

[axic]

During the ETHOnline summit @poemm gave an overview of EVM384:

[axic]

The next update discussing gas prices can be found at

EVM384 Update 5: First Gas Cost Estimates - HackMD

[poemm]

@jwasinger implemented MiMC in EVM384. https://hackmd.io/bHRfQfWaRmuIbNLTEQ6fyg?view

[jwasinger]

Here is a client implementation/benchmarking update: Go-ethereum Benchmark Update for EVM384 and Friends - HackMD . Hopefully this can help client implementers and also help to tune the pricing model. There is an issue with a compile-time blowup when I attempted to support 256 limbs as a maximum so I capped it at 128. Hopefully this is just an implementation quirk that can be fixed fairly easily by someone with more Go experience.

This is the remaining in-progress work I had with regards to EVM384 and I don’t intend to do anything else on this project in the immediate future.

[axic]

As an evolution of evm384, @jwasinger has published

EIP 5843: EVM Modular Arithmetic Extensions

This is a proposal to add EVM opcodes for efficient modular addition/subtraction/multiplication in cases where the modulus is odd, 1-1024 bits and fixed for many operations. It is an iteration from previous work on EVM384. It makes use of the following observations to construct a more efficient model for modular arithmetic operations in the EVM: If the modulus is odd and fixed for multiple operations and we also precompute some values using it, caching these and the modulus in ephemeral ca…