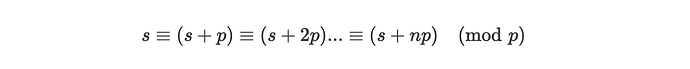EIP Draft: ZK-SNARK public inputs overflow protection
author: Beosin (eaton@beosin.com)
status: waiting for merging
type: ERC
Abstract
This standard defines that the verify function using the zk-SNARK (“Zero-Knowledge Succinct Non-Interactive Arguments of Knowledge”) algorithm needs to check the valid range of the input parameters before use. If the check passes, it returns true and continues to verify the proof. Otherwise, it returns false. The languages involved include: Solidity, JavaScript, Java, Rust, etc.
Motivation
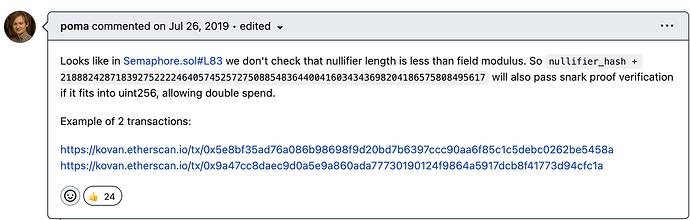
In zkp projects, if the input value range in the verify function is not properly checked, attackers can forge multiple inputs to pass the verification, causing double-spending attacks. This attack has a very wide impact, involving multiple zk-SNARK algorithms including groth16, plonk, etc., and this vulnerability exists in solidity, js and other development languages. This vulnerability was first discovered by poma on the zero-knowledge proof project Semaphore, and two successful transaction examples were given, as shown below:
Vulnerability allowing double spend · Issue #16 · semaphore-protocol/semaphore · GitHub
Subsequently, Semaphore confirmed and fixed this vulnerability. ZK libraries like ZoKrates and snarkjs also performed emergency fixes synchronously. However, Beosin security researchers found that there is currently no unified solution to this problem. For example, Semaphore protocol writes constraints into the pairing library without explicitly checking the validity range of data in the outer business logic; while the contract code generated by circom and Tornado.Cash explicitly check SNARK_SCALAR_FIELD in the verify function. This chaotic and inconsistent solution may cause confusion and security risks to many new zk DApp projects. Therefore, we hope to resolve this issue in a standardized manner.
Specification
The key words “MUST”, “MUST NOT”, “REQUIRED”, “SHALL”, “SHALL NOT”, “SHOULD”, “SHOULD NOT”, “RECOMMENDED”, “MAY”, and “OPTIONAL” in this document are to be interpreted as described in RFC 2119.
Terminology in this specification is used consistently with libsnark, as provided in that project’s README.
- Adhering Contract — A Verifier contract which adheres to this specification.
- Arithmetic circuit: An abstraction of logical statements into addition and multiplication gates.
- Proof: A
proverwho wants toproveknowledge of some secret witnessw(which satisfies an arithmetic circuit), generates aprooffrom: the circuit’s Proving Key; their secret witnessw; and its corresponding Public Inputsx. Together, a pair(proof, inputs)of satisfyinginputsand their correspondingproofforms a zk-SNARK. - Verification Key: A
trusted setupcalculation creates both a publicProving Keyand a publicVerification Keyfrom an arithmetic circuit. This interface does not provide a method for loading a Verification Key onto the blockchain. An Adhering Contract SHALL be able to accept arguments of knowledge ((proof, inputs)pairs) for at least one Verification Key. We shall call such Verification Keys in-scope Verification Keys. An Adhering Contract MUST be able to interpret unambiguously a uniqueverificationKeyIdfor each of itsin-scopeVerification Keys.
Some concepts in cryptography:
- Elliptic curve:the set of points (X,Y) that satisfies the equation y^2 = x^3 + A**x* + B is an elliptic curve.
- p:We’ll be using elliptic curves to define robust, collision resistant one-way functions, so X, Y, A, B will have all to be in a finite field (0, 1, 2, 3, …, p-1), and p needs to be a prime number > 3 (for our needs, p will be a large number).
All DApp projects using zk technology in the Ethereum ecosystem must implement this interface in their compliant verifier contract to check all inputs in a standardized, unified and secure manner:
pragma solidity ^0.5.6;
/// @title EIP-XXXX zk-SNARK public inputs Verifier Standard
/// Note: the ERC-165 identifier for this interface is 0xXXXXXXXX.
/// ⚠️ TODO: Calculate interface identifier
interface EIPXXXX /* is ERC165 & ERC1922 */ {
/// @notice Checks the arguments of Inputs are within the scalar field
/// @dev
/// MUST return `true` if Inputs passes range check (i.e. the Inputs are
/// valid).
/// MUST return `false` if the Inputs does not pass range check (i.e. if the
/// Inputs are invalid).
/// @param inputs Public inputs which accompany Proof.
/// @param p Public input which accompany the curve.
function verifyPublicInput(uint256[] inputs,uint256 p) external returns (bool result);
}
Interface
The above interface needs to be called before verify. The Reference Implementation section will introduce it using ERC1922 as an example, involving the following interfaces:
pragma solidity ^0.5.6;
/// @title EIP-XXXX zk-SNARK Verifier Standard
/// @dev See https://github.com/EYBlockchain/zksnark-verifier-standard
/// Note: the ERC-165 identifier for this interface is 0xXXXXXXXX.
/// ⚠️ TODO: Calculate interface identifier
interface ERC1922 /* is ERC165 */ {
/// @notice Checks the arguments of Proof, through elliptic curve
/// pairing functions.
/// @dev
/// MUST return `true` if Proof passes all checks (i.e. the Proof is
/// valid).
/// MUST return `false` if the Proof does not pass all checks (i.e. if the
/// Proof is invalid).
/// @param proof A zk-SNARK.
/// @param inputs Public inputs which accompany Proof.
/// @param verificationKeyId A unique identifier (known to this verifier
/// contract) for the Verification Key to which Proof corresponds.
/// @return result The result of the verification calculation. True
/// if Proof is valid; false otherwise.
function verify(uint256[] calldata proof, uint256[] calldata inputs, bytes32 verificationKeyId) external returns (bool result);
}
Rationale
To generate and verify zk-SNARK proofs on Ethereum, F_p-arithmetic finite field elliptic curve circuits need to be used, where p value determines the range of the finite field of the elliptic curve, so the input value range of the circuit is [0, 1, …, p-1]. Different curves have different p values:
BN254 curve defined in EIP-196 (also known as ALT_BN128 curve):
p = 21888242871839275222246405745257275088548364400416034343698204186575808495617
circom2 introduced two new primes, namely BLS12-381 curve:
p = 52435875175126190479447740508185965837690552500527637822603658699938581184513
And plonk2:
18446744069414584321
However, when implementing the verification code, the integer variable types in different programming languages can be much larger than the input value range of the circuit, such as: uint256 in solidity can represent [0, 2^256-1], long int in java is [-2^63,2^63-1], bigint in javascript, etc. In this case, multiple inputs can pass the verification after modulo p operation in the verification code:
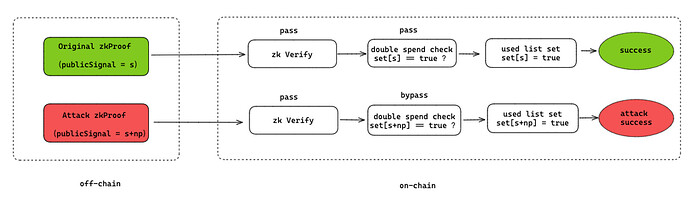
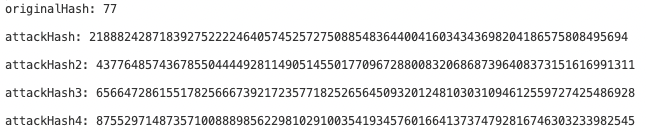
In summary, as long as any valid proof parameter x is known, values of s+np(n = 1,2,…,n) within the variable range can pass the verification. So if the attacker gets any verified x, they can construct max(uint256)/p of s’ that pass the verification. The specific attack flow is as follows:
Test Cases
This section compares the different performances against this attack in two scenarios: implementing and calling this eip interface, versus not implementing and calling the interface, to demonstrate the risks to projects.
- Assume we directly use the verify contract code for proof verification without invoking the verifyPublicInput interface in this EIP. The code is as follows:
function verify(uint[] memory input, Proof memory proof) internal view returns (uint) {
VerifyingKey memory vk = verifyingKey();
require(input.length + 1 == vk.IC.length,"verifier-bad-input");
// Compute the linear combination vk_x
Pairing.G1Point memory vk_x = Pairing.G1Point(0, 0);
for (uint i = 0; i < input.length; i++)
vk_x = Pairing.addition(vk_x, Pairing.scalar_mul(vk.IC[i + 1], input[i]));
vk_x = Pairing.addition(vk_x, vk.IC[0]);
if (!Pairing.pairingProd4(
Pairing.negate(proof.A), proof.B,
vk.alfa1, vk.beta2,
vk_x, vk.gamma2,
proof.C, vk.delta2
)) return 1;
return 0;
}
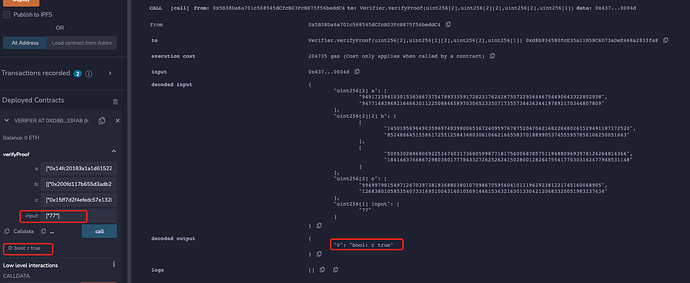
Screenshot of the original results that the proof verifiaction passed:
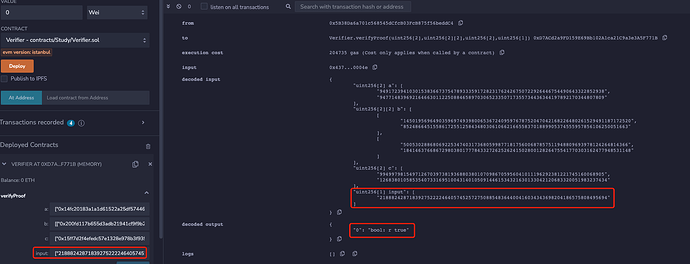
At the same time, the following 4 forged proofs can also pass the verification, causing double spending attack:
Use one of the forged proofs, the verification result is as follows:
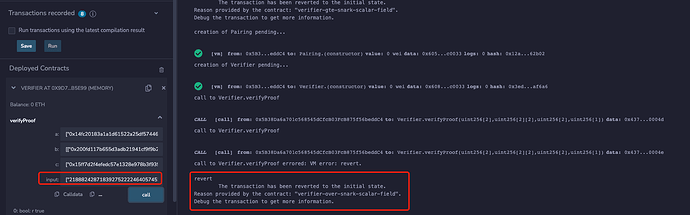
- If the verifyPublicInput interface in this eip is called, the verification of the above forged proof will fail. Part of the contract code is as follows, see Reference Implementation for details:
function verifyx(uint[] memory inputs, Proof memory proof, bytes32 verificationKeyId,uint256 p) public returns (uint){
require(verifyPublicInput(inputs,p),"verifier-over-snark-scalar-field");
require(verify(inputs,proof,verificationKeyId),"verify fail");
return true;
}
function verifyPublicInput(uint256[] inputs,uint256 p) internal view returns (bool) {
for (uint i = 0; i < input.length; i++) {
require(input < p,"verifier-gte-snark-scalar-field");
}
return true;
}
The experiment result is as shown below:
Functions
verifyPublicInput
The verify_input function forms the crux this standard. The parameters are intended to be as generic as possible, to allow for verification of any zk-SNARK:
inputsSpecified asuint256[]. As defined in ERC-1922,uint256is the most appropriate type for elliptic curve operations over a finite field.pSpecified asuint256, which corresponds to the p value of the elliptic curve used in the algorithm.
Reference Implementation
In the diagram below, zkp’s verify first checks if Inputs are within the valid range through verifyPublicInput, then calls the verify function to check if Proof is a valid proof. If yes, it returns true, otherwise it returns false. The code is as follows:
function verifyx(uint[] memory inputs, Proof memory proof, bytes32 verificationKeyId,uint256 p) public returns (uint){
require(verifyPublicInput(inputs,p),"verifier-over-snark-scalar-field");
require(verify(inputs,proof,verificationKeyId),"verify fail");
return true;
}
function verifyPublicInput(uint256[] inputs,uint256 p) internal view returns (bool) {
// uint256 p = 21888242871839275222246405745257275088548364400416034343698204186575808495617;
for (uint i = 0; i < input.length; i++) {
require(input < p,"verifier-gte-snark-scalar-field");
}
return true;
}
function verify(uint[] memory inputs, Proof memory proof, bytes32 verificationKeyId) internal view returns (uint) {
VerifyingKey memory vk = verifyingKey(verificationKeyId);
require(input.length + 1 == vk.IC.length,"verifier-bad-input");
// Compute the linear combination vk_x
Pairing.G1Point memory vk_x = Pairing.G1Point(0, 0);
for (uint i = 0; i < input.length; i++) {
vk_x = Pairing.addition(vk_x, Pairing.scalar_mul(vk.IC[i + 1], input[i]));
}
vk_x = Pairing.addition(vk_x, vk.IC[0]);
if (!Pairing.pairingProd4(
Pairing.negate(proof.A), proof.B,
vk.alfa1, vk.beta2,
vk_x, vk.gamma2,
proof.C, vk.delta2
)) return 1;
return 0;
}
Reference
- Snarkjs.Circom 2 Documentation. Installation - Circom 2 Documentation
- Zcash. What are zk-SNARKs? What are zk-SNARKs? - Z.Cash
- Vitalik Buterin. zk-SNARKs: Under the Hood. Zk-SNARKs: Under the Hood. This is the third part of a series of… | by Vitalik Buterin | Medium
- Christian Reitweissner. zk-SNARKs in a Nutshell. zkSNARKs in a nutshell | Ethereum Foundation Blog
- Ben-Sasson, Chiesa, Tromer, et. al. Succinct Non-Interactive Zero Knowledge for a von Neumann Architecture. https://eprint.iacr.org/2013/879.pdf
- libsnark: A C++ Library for zk-SNARKs (“project README)”. GitHub - scipr-lab/libsnark: C++ library for zkSNARKs
- ZoKrates: Scalable Privacy-Preserving Off-Chain Computations. Wirtschaftsinformatik - TU Berlin
- ZoKrates Project Repository. GitHub - Zokrates/ZoKrates: A toolbox for zkSNARKs on Ethereum
- Joseph Stockermans. zkSNARKs: Driver’s Ed. GitHub - jstoxrocky/zksnarks_example: zkSNARKS tutorial
- Christian Reitweissner - snarktest.solidity. zkSNARKs test code · GitHub