EIP-7054: Gas Efficient Square Root Calculation with Binary Search Approach

ERCs
,
1

eip: 7054
title: Gas Efficient Square Root Calculation with Binary Search Approach
description: A gas-optimized sqrt function for efficient square root computation in Solidity, replacing algorithms based on the Babylonian method.
author: hiddenintheworld.eth (@hiddenintheworld)
discussions-to: EIP-7054: Gas Efficient Square Root Calculation with Binary Search Approach
status: Draft
type: Standards Track
category: ERC
created: 2023-06-02
requires: None

Abstract

The proposal introduces a gas-efficient function for computing square roots in Solidity, aiming to replace current algorithms based on Newton’s method.

This EIP introduces a new and more efficient approach to computing the square root in Solidity using a binary search algorithm. It optimizes the number of iterations required for computation, resulting in reduced gas consumption while maintaining accurate results. The proposal details the implementation of this algorithm in Solidity, which involves bit-wise operations and decision branching. This method not only provides a more optimal way for square root calculations but also reduces the overall computational complexity, thereby enhancing the performance and efficiency of contracts that require such calculations.

Motivation

Many Ethereum contracts, including widely used protocols like Uniswap, require square root computations. These computations are commonly performed using a variant of Newton’s method - the Babylonian method. However, we propose to replace it with a more efficient algorithm for calculating square root, that operates based on Binary search using bitwise shifts.

The primary motivation behind this proposal is to optimize gas usage in Ethereum contracts involving square root computations. The proposed function has a constant number of iterations (seven) independent of the input size. This signifies potential gas efficiency for large inputs, in stark contrast to Newton’s method variants, which may require more iterations for larger numbers or non-perfect squares.

Furthermore, in high-traffic protocols like Uniswap V2, square root calculations are invoked at least twice per token swap operation. With the enormous volume of token swaps happening daily, adopting this more efficient square root calculation method could lead to substantial gas savings across the network, enhancing overall transaction efficiency. Therefore, the implementation of this method carries significant importance, contributing to Ethereum’s scalability and efficiency.

Potential Applications

Apart from token swapping protocols like Uniswap V2, the proposed sqrt function could also be beneficial in a variety of other Ethereum contracts, including but not limited to:

  1. Financial Derivatives Contracts: In DeFi, many financial derivatives require the calculation of square roots for determining option prices, volatilities, and other key financial metrics. The proposed sqrt function’s efficiency in handling larger numbers could be highly beneficial in such contracts.
  2. Gaming Contracts: In Ethereum-based gaming and NFT platforms, square root computations are often required for calculating game metrics or token distributions. Implementing this proposal can enhance performance and gas efficiency.
  3. DAO Voting Systems: Square root voting, where voting power is proportional to the square root of the number of tokens held, has been proposed as a way to limit the influence of large token holders. The proposed method can make such voting systems more efficient.

Specification

The new sqrt function, proposed for calculating the square root of an unsigned 256-bit integer, is as follows:

function sqrt(uint256 x) public pure returns (uint128) {
    if (x == 0) return 0;
    else{
        uint256 xx = x;
        uint256 r = 1;
        if (xx >= 0x100000000000000000000000000000000) { xx >>= 128; r <<= 64; }
        if (xx >= 0x10000000000000000) { xx >>= 64; r <<= 32; }
        if (xx >= 0x100000000) { xx >>= 32; r <<= 16; }
        if (xx >= 0x10000) { xx >>= 16; r <<= 8; }
        if (xx >= 0x100) { xx >>= 8; r <<= 4; }
        if (xx >= 0x10) { xx >>= 4; r <<= 2; }
        if (xx >= 0x8) { r <<= 1; }
        r = (r + x / r) >> 1;
        r = (r + x / r) >> 1;
        r = (r + x / r) >> 1;
        r = (r + x / r) >> 1;
        r = (r + x / r) >> 1;
        r = (r + x / r) >> 1;
        r = (r + x / r) >> 1;
        uint256 r1 = x / r;
        return uint128 (r < r1 ? r : r1);
    }
}

Rationale

The proposed function brings forth an improved method for square root calculations, reducing gas costs in smart contracts by leveraging a binary search mechanism and bitwise shifts, which guarantee constant iterations irrespective of the input size.

Backwards Compatibility

This proposal poses no backwards compatibility issues, as it only provides a more efficient methodology for calculating square roots in Solidity.

Implementation

The implementation requires running instances of the Babylonian square root function and the proposed sqrt function in the relevant contracts.

pragma solidity ^0.8.0;

contract SqrtComparison {
    function BinarySearchSquareRoot(uint256 x) public pure returns (uint128) {
        if (x == 0) return 0;
        else{
            uint256 xx = x;
            uint256 r = 1;
            if (xx >= 0x100000000000000000000000000000000) { xx >>= 128; r <<= 64; }
            if (xx >= 0x10000000000000000) { xx >>= 64; r <<= 32; }
            if (xx >= 0x100000000) { xx >>= 32; r <<= 16; }
            if (xx >= 0x10000) { xx >>= 16; r <<= 8; }
            if (xx >= 0x100) { xx >>= 8; r <<= 4; }
            if (xx >= 0x10) { xx >>= 4; r <<= 2; }
            if (xx >= 0x8) { r <<= 1; }
            r = (r + x / r) >> 1;
            r = (r + x / r) >> 1;
            r = (r + x / r) >> 1;
            r = (r + x / r) >> 1;
            r = (r + x / r) >> 1;
            r = (r + x / r) >> 1;
            r = (r + x / r) >> 1;
            uint256 r1 = x / r;
            return uint128 (r < r1 ? r : r1);
        }
    }
    
    function BabylonianSquareRoot(uint y) public pure returns (uint z) {
        if (y > 3) {
            z = y;
            uint x = y / 2 + 1;
            while (x < z) {
                z = x;
                x = (y / x + x) / 2;
            }
        } else if (y != 0) {
            z = 1;
        }
    }
}

Security Considerations

The proposed method does not introduce any new security risks as it is just an algorithm to calculate the square root of a given input.

Test Cases

The test is conducted in solidity version 0.8.18 with the Solidity Optimizer value of 200.

The following test cases demonstrate the efficiency and accuracy of the proposed function as compared to the traditional Babylonian method for various inputs:

  1. For an input of 0, both the proposed and Babylonian method return 0. In terms of gas usage, the proposed used 292 gas whereas Babylonian method used 335 gas.
  2. For an input of 1, both methods return 1. The proposed function used 1617 gas, and the Babylonian method used 339 gas.
  3. For an input of 50, both methods return 7. The proposed function used 1641 gas, and the Babylonian method used 1495 gas.
  4. For an input of 105, both methods return 10. The proposed function used 1746 gas, and the Babylonian method used 1641 gas.
  5. For an input of 115792089237316195423570985008687907853269984665640564039457584007913129639935, both methods return 340282366920938463463374607431768211455. The proposed used 1767 gas, and the Babylonian method used 34376 gas.

These test cases clearly demonstrate the accuracy of the proposed function. While the gas usage is higher for smaller inputs, for inputs 105 and greater, the proposed function uses significantly less gas than the Babylonian method.

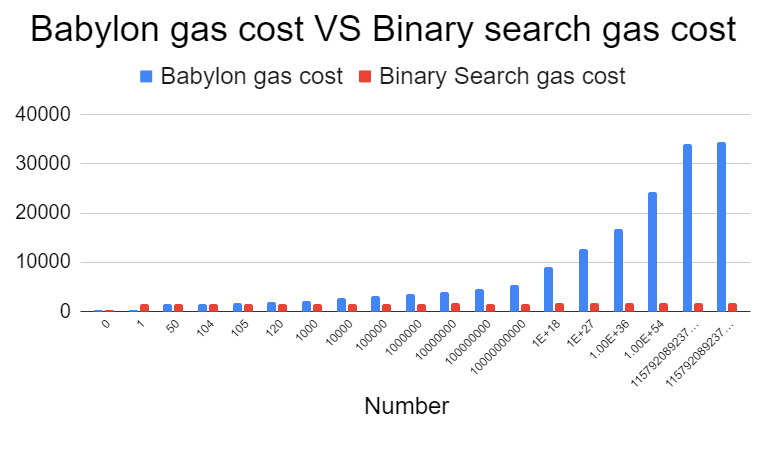
Below is a table of the gas cost with a different number as input for the Babylonian method and the proposed method:

Number Babylonian gas usage Proposed method gas usage
0 335 292
1 339 1617
50 1495 1641
104 1495 1641
105 1746 1641
120 1997 1641
1000 2248 1631
10000 2750 1665
100000 3252 1641
1000000 3503 1647
10000000 4005 1671
100000000 4507 1665
10000000000 5511 1641
1E+18 9025 1695
1E+27 12790 1679
1E+36 16806 1719
1E+54 24336 1695
115792089237316195423570985008687907852589419931798687112530834793049593217025 34125 1767
115792089237316195423570985008687907853269984665640564039457584007913129639935 34376 1767

Below is a plotted chart of gas cost when comparing the Babylonian method and the proposed method:

gas_compare
gas_compare765Ă—457 14.5 KB

Gas estimation

In our extensive testing, we found significant gas cost reductions when using the proposed Binary Search-based square root function compared to the traditional Babylonian method.

Here is a comparative breakdown of gas usage based on a variety of inputs(see table in Test Cases):

  • For an input of 0, the Babylonian method required 335 gas, while the proposed method required 292 gas.

  • For an input of 1, the Babylonian method used 339 gas, whereas the proposed method consumed 1617 gas.

  • Starting from an input value of 105, the proposed method consistently used less gas than the Babylonian method. As an example, at input 105, the proposed method used 1746 gas, while the Babylonian method used 1641 gas.

  • When testing the large input of 115792089237316195423570985008687907853269984665640564039457584007913129639935, the Babylonian method required approximately 34376 gas while the proposed method only needed about 1767 gas.

The difference in gas cost appears to increase with the size of the input. This suggests that the proposed function provides superior efficiency for larger inputs. However, this is an estimate, and actual gas costs may vary depending on the specifics of the implementation and the Ethereum network.

To further illustrate the savings, we introduce the concept of Percentage Reduction in gas costs (PR). This is calculated by the formula:

PR = ((Gas used by Babylonian Method) - (Gas used by the proposed method)) / (Gas used by Babylonian Method) * 100

For example, using the large input of 115792089237316195423570985008687907853269984665640564039457584007913129639935, we calculate:

PR = (34376 - 1767) / 34376 * 100 %
PR = 94.86 % (rounded to 2 significant decimal places)

This indicates that for this input size, the proposed function leads to a 94.86% reduction in gas cost compared to the Babylonian method. This makes a compelling case for its adoption in contexts where efficient computation is crucial. Nonetheless, it is recommended to conduct detailed tests and benchmarks to validate these estimations.

Drawback

Since for input below 105, there are cases that the proposed function consumes more gas.

For example, using the input of 104, we calculate:

PR = (1495 - 1641) / 1495 * 100 %
PR = -0.098% (rounded to 2 significant decimal places)

Using the input of 1, we calculate:

PR = (339 - 1617) / 339 * 100 %
PR = -376.99 % (rounded to 2 significant decimal places)

It is founded that the maximum drawback occurs when the input is 1, the proposed function has an increase of +376.99% in gas cost compared to the Babylonian method.

Gas Cost Analysis

From the test cases and data table, it can be observed that the proposed function uses more gas for smaller inputs (below 105) but is more gas-efficient for larger inputs.

This indicates that there exists a trade-off point, where the proposed method becomes more gas-efficient than the Babylonian method. The trade-off point lies around the input value of 105.

This information is significant for developers and contracts to decide whether to implement the proposed function. In scenarios where contracts deal predominantly with smaller numbers (below the trade-off point), the Babylonian method may still be a more gas-efficient option. However, for contracts handling larger numbers (greater than the trade-off point), the proposed function can result in substantial gas savings.

Conclusion

While the proposed method has its trade-offs, it is evident that in most scenarios where larger numbers are more frequent, such as token swapping, the usage of this proposed function can be more efficient and beneficial.

Copyright

Copyright and related rights waived via CC0.

2 Likes
2

This should be used in all computers.

3

What method is used by the pending UniswapV4 implementation?

4

looks impressive on high numbers.
but why not have a condition to use different algorithm for small (e.g <100) values? This way, with a very slight increase in gas usage for high numbers (a single compare) you end up improving gas cost for all values.

5

Those situations are not necessarily more common, and conditioning on that is not free. There is cost-benefit analysis to do. I expect that, for most scenarios where you would sqrt a uint256, the parameter is expected to be in the range where the babylonian method is worse.

6

Why is the last if testing against 0x8 rather than 0x4? My understanding is that you want to compute 2^(log2(x) / 2), and 0x4 would give the correct result on all values.

7

The sqrt function is here in line 910, not exactly Binary Search but still efficient (same logic as proposed with 7 iterations), maybe the devs already read this thread and take it as a reference.

function sqrt(bytes16 x) internal pure returns (bytes16) {
        unchecked {
            if (uint128(x) > 0x80000000000000000000000000000000) {
                return NaN;
            } else {
                uint256 xExponent = uint128(x) >> 112 & 0x7FFF;
                if (xExponent == 0x7FFF) {
                    return x;
                } else {
                    uint256 xSignifier = uint128(x) & 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFF;
                    if (xExponent == 0) xExponent = 1;
                    else xSignifier |= 0x10000000000000000000000000000;

                    if (xSignifier == 0) return POSITIVE_ZERO;

                    bool oddExponent = xExponent & 0x1 == 0;
                    xExponent = xExponent + 16383 >> 1;

                    if (oddExponent) {
                        if (xSignifier >= 0x10000000000000000000000000000) {
                            xSignifier <<= 113;
                        } else {
                            uint256 msb = mostSignificantBit(xSignifier);
                            uint256 shift = (226 - msb) & 0xFE;
                            xSignifier <<= shift;
                            xExponent -= shift - 112 >> 1;
                        }
                    } else {
                        if (xSignifier >= 0x10000000000000000000000000000) {
                            xSignifier <<= 112;
                        } else {
                            uint256 msb = mostSignificantBit(xSignifier);
                            uint256 shift = (225 - msb) & 0xFE;
                            xSignifier <<= shift;
                            xExponent -= shift - 112 >> 1;
                        }
                    }

                    uint256 r = 0x10000000000000000000000000000;
                    r = (r + xSignifier / r) >> 1;
                    r = (r + xSignifier / r) >> 1;
                    r = (r + xSignifier / r) >> 1;
                    r = (r + xSignifier / r) >> 1;
                    r = (r + xSignifier / r) >> 1;
                    r = (r + xSignifier / r) >> 1;
                    r = (r + xSignifier / r) >> 1; // Seven iterations should be enough
                    uint256 r1 = xSignifier / r;
                    if (r1 < r) r = r1;

                    return bytes16(uint128(xExponent << 112 | r & 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFF));
                }
            }
        }
    }
8

You are right, should fix it.

9

Hey, has this been passed?
Why not just use uint256’s SQRT function on EVM?
So basically add an SQRT opcode and geth EVM can use uint256 Sqrt function directly.

1 Like
10

It’s a clever approach!

A workaround for the small numbers could be the byte YUL operation, for 3 gas it returns the N-th byte of the word. If x < 32, you could just return the x-th byte of the lookup table with the hardcoded results.

It may make sense to do another lookup for x >= 32 && x < 64 using x-32 and a table with square roots for numbers 32-63. It may be done efficiently with add(byte(x, lookup_0_31), byte(sub(x, 32), lookup_32_63)), because byte returns 0 for indexes not in range 0-31, and sub(x,32) will underflow for values smaller than 32.

Branches are expensive, it may be cheaper to change the if (xx >= 0x100000000000000000000000000000000) { xx >>= 128; r <<= 64; } parts with a branchless equivalent. Here’s an example, unfortunately it’s the easiest to do using YUL since Solidity doesn’t support converting bool to uint:

uint256 isGt;
assembly {
    isGt := gt(xx, 0xffffffffffffffffffffffffffffffff)
}
xx >>= isGt << 7;
r <<= isGt << 6;

It may also be beneficial to rewrite all the divisions in YUL, because in Solidity it’s impossible to disable the division by zero check, and the compiler almost certainly is not smart enough to skip it as impossible to trigger. The additions should also benefit from YUL or at least unchecked blocks, so the compiler doesn’t check for the overflows, which are impossible here.

Would it be correct to replace:

uint256 r1 = x / r;
return uint128 (r < r1 ? r : r1);

with yet another:

return (r + x / r) >> 1;

? It should be if the distance between r and r1 is at most 1. If so, it may save some gas on the jumps.

12

Hi, I implemented a branchless version of the SQRT function, which have a constant gas cost of 355 in evm assembly, or 407 in YUL inline assembly.

gist.github.com/Lohann/f01e2558691ba8648f1e5a7c6e8d37da

pragma solidity >=0.7.0 <0.9.0;


contract Sqrt {

    // Branchless sqrt with constant gas cost ~407 + solidity overhead
    function sqrt(uint256 x) public pure returns (uint256 r) {
        assembly ("memory-safe") {
            // r = floor(log2(x))
            r := shl(7, gt(x, 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF))
            let xx := shr(r, x)

            let rr := shl(6, gt(x, 0xFFFFFFFFFFFFFFFF))
            xx := shr(rr, xx)
            r := or(r, rr)

            rr := shl(5, gt(xx, 0xFFFFFFFF))
            xx := shr(rr, xx)
            r := or(r, rr)

            rr := shl(4, gt(xx, 0xFFFF))
            xx := shr(rr, xx)
            r := or(r, rr)

            rr := shl(3, gt(xx, 0xFF))
            xx := shr(rr, xx)
            r := or(r, rr)

            rr := shl(2, gt(xx, 0x0F))
            xx := shr(rr, xx)
            r := or(r, rr)

            rr := shl(1, gt(xx, 0x03))
            xx := shr(rr, xx)
            r := or(r, rr)
            
            r := shl(shr(1, r), 1)
            
            // Newton's method
            r := shr(1, add(r, div(x, r)))
            r := shr(1, add(r, div(x, r)))
            r := shr(1, add(r, div(x, r)))
            r := shr(1, add(r, div(x, r)))
            r := shr(1, add(r, div(x, r)))
            r := shr(1, add(r, div(x, r)))
            r := shr(1, add(r, div(x, r)))

            // r = min(r, x/r)
            r := sub(r, gt(r, div(x, r)))
        }
    }
}
1 Like