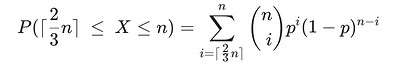Hi, magicians, I have some ideas to convert sharding solution of ETH2 to a new rollup approach, which can be called Collaborative Rollup(coRollup for short). It will achieve fast finality without zkEVM.
Background
Sharding has been discussed for a long time since ETH2 was proposed. After danksharding was come up with, the community seemed to reach a consensus on data sharding, leaving the execution to L2(Rollups), and the original design of execution sharding with multi-committees was rarely talked about anymore due to its complexity. But I think the execution sharding should still be studied in depth and some of its properties can still be in use, especially its security model.
In this post, I will propose Collaborative Rollup, a new type of Rollup that is based on multi-committees derived from the execution sharding scheme and thus has the same security model. In contrast with ZK Rollup, it can easily have full EVM compatibility while some opcodes are still hardly resolved in zkEVM. In terms of Optimistic Rollup, thereβs no need for a long challenging period in Collaborative Rollup.
Overview
The key components of Collaborative Rollup consist of Producer Node(PN), Endorsor Node(EN), Management Contract(MC), and State Contract(SC).
One can stake tokens and register its public key(BLS) to MC to be PN or EN. We will select top N ENs by the amount of staking, and randomly shuffle them into M committees by a trusted random source like RANDAO or VRF, etc. That info of committees is also managed by MC.
PN collects L2 transactions in packets, generates execution results by running transactions in EVM, and sends the results to the committees of EN for endorsement. EN verifies the results by actually executing the transactions in its local EVM. If the results are valid, EN signs the results as an endorsement and broadcasts them. EN collecting endorsements of at least 2/3 ENs in a committee can aggregate these BLS signatures as proof, and commit execution results, proof, and transactions to the chain as other Rollup does.
ββββββ
Client -> β PN β ββββββ
ββββββ β
V
ββ β β β β β β β β β β β β ββ β β β β β β β ββ β β β β β β β
β ββββββ ββββββ ββββββ β β β β β
β β EN β β EN β β EN β β β Committee 2 β ... β Committee n β
β ββββββ ββββββ ββββββ β β β β β
ββ β β β β β β β β β β β β ββ ββ β β β β β β ββ ββ β β β β β β
Committee 1 β
V
ββ β β β β β β β β β β β β β β β β β β β β β β β β β β β ββ
β ββββββ ββββββ ββββββ β
β ... βββββ L1 βββββββββββββ L1 ββββββββββββ L1 ββββ ... β
β ββββββ ββββββ ββββββ β
ββ β β β β β β β β β β β β β β β β β β β β β β β β β β β β
Security Model
As described above, the security model of Collaborative Rollup relies on endorsements of a random committee as the original execution sharding of ETH2 did. It is well known that a single node cannot be trusted, whereas a group of randomly selected ones can be. If we assume that less than 1/3 of the total nodes are malicious and the majority of a committee is 2/3, then safety can be held only if malicious nodes cannot gain the majority in a single committee.
Next, the probability of malicious nodes gaining the majority in a committee will be estimated. Let N be the size of total nodes, in which K of them are malicious. And n is the committee size, k of which are adversaries, so the probability distribution of the number of malicious nodes in one committee can be modeled as a hypergeometric distribution:
P(X=k) = Combination(K, k) * Combination(N-K, N-n) / Combination(N, n)
The probability wanted follows cumulative hypergeometric distribution, which, when N is large, degrades to binomial distribution:
In which p is 1/3. We can see that when n is large enough, the probability that malicious nodes gain the majority in a committee is negligible. Also, the majority can be interpreted as staking shares, just as POS. Here are some examples of the probability:
n = 32 -> P = 0.000045
n = 64 -> P = 0.000000033
n = 128 -> P = 0.0000000000000056
On the other hand, if an endorsement that contains illegal verifications gets signed by some faulty node, no matter whether it could get adequate signatures to commit to L1, the signed invalid endorsement itself can be treated as fraud proof and committed to L1 to punish the signing node, which is a 1-of-N trust mode.
Endorsement and Validation
The states in L2 can be organized as a Verkle tree, which uses KZG as its state commitment and also implements trie just as MPT. Therefore, the state root is the commitment of the whole tree. We use Verkle tree here because it has smaller proofs than Merkle tree(O(logN) vs. O((k-1)logN)), given a k-ary tree of N leaves).
After PN executed transactions in its local EVM, we can get the input states, output states, and the output state root. Then the execution result can be formatted as follows
ββ β β β β β β β β β β β β β β β β β β β β β β β β β β β β β β β β β β β
β PN Signature β
β ββββββββββββββββββ¬ββββββββββ¬βββββββββββββββββββ¬βββββββββββββββββββββ β
β β ENDORSEING_FEE β TX_ROOT β INPUT_STATE_ROOT β OUTPUT_STATE_ROOT β β
β ββββββββββββββββββ΄ββββββββββ΄βββββββββββββββββββ΄βββββββββββββββββββββ β
ββ β β β β β β β β β β βββ β β β β βββ β βββ β β β β β β β β β β β β β β
βββββββββββββββββ βββββββββ βββββββββββ
V V V
ββ β β β β β β β β β β β β β β β β β β β β β β β β β
β Transactions β β Input states β β Output states β
ββ ββ β β β β β β ββ ββ β β β β β β β β β β β β β β β
The execution result consists of endorsing fee info, last state root, state root of the result, Merkle root of transactions, alongside related input states and Verkle proofs, Verkle path of output states belonging to last state root, transactions needed to be executed, and signatures of the three roots and endorsing fee info above.
When EN receives an execution result produced by a qualified PN, it first checks if it has the last state root, then verifies Verkle proofs of input states as well as paths of output states. If all of the above are valid, we will have a partial state tree that includes all the states needed. After that, check the transactions Merkle root and run all transactions with local EVM on top of that state tree to generate the output state tree. Lastly, check whether the root of the output state tree is equal to that in the execution result. If it is true, generate endorsement by signing the data of the three roots in the execution result as well as the status of value 1. Otherwise, the ENs will sign data of the same content above except that the status is 0.
ββ β β β β β β β β β β β β β β β β β β β β β β β β β β β β β β β β β β β β β β
β SN Signature β
ββ β β β β β β β β β β β β β β β β β β β β β β β β β β β β β β ββ β
β PN Signature β β
β ββββββββββββββββ¬ββββββββββ¬βββββββββββββββββ¬ββββββββββββββββββ β ββββββββββ β
β βENDORSEING_FEEβ TX_ROOT βINPUT_STATE_ROOTβOUTPUT_STATE_ROOTβ β β STATUS β β
β ββββββββββββββββ΄ββββββββββ΄βββββββββββββββββ΄ββββββββββββββββββ β ββββββββββ β
ββ β β β β β β β β β β β β β β β β β β β β β β β β β β β β β β ββ΄β β β β β β β
Any signing EN who receives endorsements from 2/3 of a committee can aggregate the signatures in endorsements into one to form the final endorsement and commit it to L1 with contract calling transactions just as other rollups do. The L1 chain checks the endorsement by verifying the signature as well as the Merkle root of transactions in the endorsement. If they are both valid and the status is 1, the rollup transaction will be accepted and the state root will be set into SC.
Fees and Incentive
As described above, the transaction fee of committing to L1 will be paid by EN. One more thing that needs to be mentioned is that there is endorsing fee info in the execution result sent to EN to be endorsed. There is an endorsing fee account for each PN in SC used for paying that. EN will check the account balance to determine whether it is sufficient to pay the fee set in the execution result to be endorsed. Some proportion of the endorsing fee will be taken to the EN who successfully sends the transaction of endorsement to L1, and all ENs signing the endorsement(including the one sending transaction above) will share the rest of the fee equally.
The endorsing fee info can be designed to include GAS_PRICE and GAS_LIMIT as well. No matter whether the execution result is valid or not, SNs can collect signatures of 2/3 of a committee and commit to L1 to charge for endorsing fees.
Also, as stated above, we have a mechanism of fisherman. Any invalid endorsement, no matter whether it has been committed to L1 or not, could be proof of maliciousness and sent to L1 by any node. The stake of ENs who have backed up the faulty endorsement will be slashed and some proportion of the slashed stake will be given to the proof-sending node as an incentive.