Oh and to somehow couple ERC-7573 and ERC-6123, it would also be easier to use int256 as transactionID type cause the ISDC.afterTransfer also uses uint256 as its transactionID so you could take advantage of this pattern.
1 Like
I could not answer all the aspects that were brought up here due to some overload. Sorry for that.
We made some minor updates to the ERC 7573 since its initial version. To summarize:
-
The ILockingContract now can now use a hashing for the key (instead of using the encrypted key). Hence, for any key K there will be a pair E(K), H(K). This concept was already described in the initial version of the paper, but the argument “encryptedKey” was re-used with the “hashedKey”. We added two separate argument. This also allows that the corresponding event emits the pair E(K), H(K).
-
The IDecryptionContract event TransferKeyReleased has an additional argument “sender”. In our white paper, we describe using multiple decryption oracles performing partial decryption (c.f. threshold encryption). To distinguish the different decryption oracles, the TransferKeyReleased event carries the additional argument “sender”.
-
Following Julius suggestion to change byte32 to uint256.
-
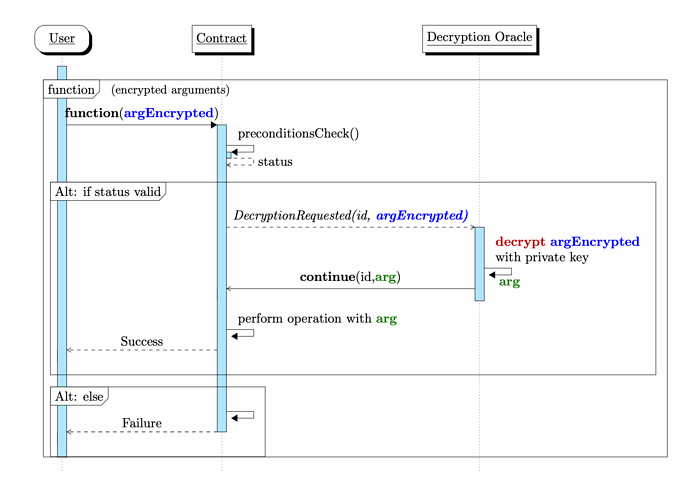
In the white paper we propose a key format and an implementation for the decryption oracle that ensures that only keys originating from eligible contracts are decrypted. In addition, we discuss the optional functionality that the decryption oracle can provide encrypted keys . By this, the users do not need to know any details of the encryption method. We elaborate on the aspect that the encryption oracle is a requirement originating from a fundamental property common to (most) blockchains: that argument values can be observed before code execution.
The contracts are available at “@finmath.net/dvp”: “0.3.1”
1 Like
To some extend an off-chain decryption is a requirement that stems from a property that is common to (most) blockchains: That function arguments can be observed prior to function execution. For the DvP this results in a race condition. We tried to illustrate this in the white paper.
Hi @cfries, I have a question regarding encryption. In a real-world implementation, should there be a function to identify which encryption algorithm is being used for a trade?
example idea from ERCs/ERCS/erc-7627.md at master · ethereum/ERCs · GitHub
Dear M
This is a very good point. Thank you.
For the DvP protocol, transparency on the encryption method is not a prerequisite if the decryption oracle generates the encrypted key (for example, it could store the encryption method as part of the byte sequence of the encrypted key) - if the decryption oracle contract handles generation and decryption, the specific method is rather an implementation detail.
But more important is transparency on the hashing algorithm, because the hashing algorithm used in the ILockingContract (for the unlocking) has to match the one used by the decryption oracle.
Here, users should be aware of the hashing algorithm utilized by a specific decryption oracle address.
But yes, one might add something that allows one to query this information.
Best
C.
A public test deployment of the ERC-7573 Decryption Oracle is available on Polygon PoS (mainnet), Amoy Polygon (testnet), and Ethereum (mainnet).
On-chain proxy contract to off-chain decryption service with three request types: generate, verify, and decrypt.
Contract:
Polygon mainnet at 0x918a98c0aef96c71f3cb4f66a476049c7caac028
Ethereum mainnet at 0x31012A98CD55F13dd65Fe9bb388676130B38d1B1
Amoy / Polygon testnet at 0xD63D5963deb026ad477265BF631F52cF6ca431AC
Try the flow in Remix (see finmath-decryption-oracle ). Feedback is welcome.