EIP-7918: Blob base fee bounded by execution cost

[aelowsson]

@dataalways

Thank you for the proposal. I like the idea and definitely think we should explore the solution space. I have a few question:

Thanks for your question and your analytical work on blob base fees, which has been very valuable.

Question 1: Coupling of fee markets

@dataalways

This seems to be moving towards recoupling the two fee markets, is that something that we want? Like the two are already often entangled because demand drivers on one layer tend to drive demand on the others as well (i.e., price volatility driving more defi usage), but do we want to explicitly increase the entanglement?

The price of blobspace depends on the price of execution gas, and this should be reflected in the fee market. Currently, the mechanism behaves as follows:

• Users purchase blobspace by spending execution gas and blob gas.
• The blob gas fee update mechanism is unaware of the cost of execution gas, and thus unaware of the cost of blobspace.
• A relatively high cost of execution gas renders changes to the blob gas fee subordinate in determining quantity demanded.
• The mechanism fails to timely converge on equilibrium whenever the cost of execution gas dominates the cost of blob gas.

In essence, the mechanism behaves as if it controlled the price of blobspace when it only controls the price of blob gas. EIP-7918 resolves this by adjusting the auction mechanism when the cost of execution gas dominates. The two fee markets still remain fully independent in the operational range where the blob base fee carries the price signal.

Question 2: Alternative designs

@dataalways

If we’re tying the two markets together, why did you choose this value? Does it make sense to tie the price to additional liveness risk of including blobs instead?

I am not sure what exact value you are referring to? A nice thing about this proposal is its minimalist nature. Fee parity and amortization across target blobs was the most neutral condition I could think of. The only other option I considered was amortization across max blobs instead of target blobs. I think both options are perfectly valid but favored target blobs for two reasons:

• It represents the equilibrium condition and can thus be perceived as slightly more neutral.
• It results in a slightly higher fee parity threshold, both in terms of its nominal level (see Figure 1 below) and the relative level that more execution-gas-intensive blob consumers operate on. Concerning the relative level, we can focus on the bump centered at around 126k in your informative analysis of execution gas used by block submitters. A gas-intensive L2 submitting a single blob would uses (6/1) × (21k/126k) = 36 times more execution gas than blob gas under Pectra settings before the bound on blob gas activates. With amortization across max blobs, the outcome is (9/1) × (21k/126k) = 54.

Concerning tying the price to liveness risk, I suppose it can make sense, but it is not something I have explored.

I have considered one other option, which I call a composite fee market. This would however be a much bigger change, also conceptually. It is not something we should be pursuing right now and would have to be part of a potential future harmonization of fee markets. The design can however be informative also for understanding EIP-7918, and it is therefore described briefly below.

Composite fee market

The composite fee market updates the blob base fee based on the real demand function for blobspace, as previously specified in EIP-7918:

        Q(b + c).

In this equation, the long-run average per-block quantity of blobs demanded Q depends on the blob base fee b and the tx cost c, expressed per blob gas as specified in the EIP. The real demand function will reflect variations in blob submission strategies, but the same estimate for c as in EIP-7918 could potentially be used. Other options are to simply compute c for every block or to specify c as the long-run average.

Let q represent the desired fractional shift in the cost of blobspace, e.g., in the range [-0.125, 0.125], computed from the realized Q of the block and the target quantity for a block. Further, let c₀ define the tx cost of the previous slot, computed according to one of the options of the previous paragraph and expressed per blob gas. The composite fee auction then updates from b₀ to b₁ by accounting for c₀:

        b₁ = b₀ + q(b₀ + c₀)

To the user that employs the same execution gas per blob gas as in c₀, the maximal change in cost of blobspace per slot would still be 12.5%. The proportional change in b can however be dramatic whenever b << c. This is as intended, allowing the composite fee auction to quickly converge on equilibrium, no longer “getting stuck” at lower blob base fees.

As a general comment: to devise a sound fee market, it is important to model the real demand function.

Question 3: Comparison with EIP-7762

@dataalways

The main blocker for EIP-7762 was a desire not to tinker with the blob fee market and not to add more complexity to Pectra. This seems more complicated than 7762 and the benefits over 7762 aren’t that clear to me. If in the long-term we want to have blob capacity > demand to keep price stability but then charge L2s a small amount, then wouldn’t it be better to have a fixed base fee that is easier to justify tuning?

The fee mechanism is currently unaware of the full price of the goods that it attempts to regulate the price for. It therefore fails to converge on equilibrium in a timely manner. To resolve this, the fee update should be made aware of the price of execution gas. The main blocker against EIP-7762 is arguably that it does not relay this price signal but instead specifies a hard-coded price floor. Such a fixed floor could perhaps be characterized as “tinkering”, and this was potentially why the EIP had difficulties gathering consensus. If the price of execution gas becomes much lower, say between 2**5 to 2**6 wei, it is hard to imagine that the price floor for blob gas of 2**25 wei specified in EIP-7762 would be considered appropriate. A price floor that adapts with the price of execution gas is more neutral. It can then adapt with the actual cost of blobspace to ensure a functioning fee market, while letting the price of blob gas evolve without restrictions within these technical limits. Framed within the current “price discovery” discourse, EIP-7918 identifies the inelasticity horizon as an impediment to effective “price discovery”, and keeps the price of blob gas sufficiently high to always influence blobspace equilibrium formation.

EIP-7762 indeed takes the cost of execution gas as its starting point:

To set the parameter apropriately, one aproach is to look at the cost of simple transfers when base fees are low. The cost of a simple transfer when the base fee is 1 GWEI is ~5 cents USD at today’s prices (2,445.77$ ETH/USDC). We can try to peg the minimum price of a blob to that.

One difference is that EIP-7918 allows this type of comparison to take place automatically every block, such that the protocol no longer needs to rely on developers to adjust the floor, should the cost of execution gas change going forward. You mention that the fixed floor of EIP-7762 makes it easier to justify tuning the floor to keep price stability, but I would argue that this is rather a drawback. A self-adjusting dynamic floor is the ideal to strive towards. I would further argue that the change is specifically to ensure a functioning fee market, as opposed to the protocol charging L2s some specific amount for blob gas. EIP-7918 will indeed increase protocol income, just like EIP-7762, but this is mainly a necessity to allow the protocol to operate under more stable resource consumption, without having longer periods of successive blocks consuming above-target blob gas.

A second difference is that EIP-7918 accounts for the potential to amortize the cost of execution gas across blobs when setting the floor. It is reasonable to account for improved future gas efficiency derived via scaling. As stipulated in the EIP:

@aelowsson

To understand why potential future blob scaling is important to account for when designing the mechanism, consider how the price of storing a fixed amount of data has fallen over the last 80 years.

The discussion regarding the fixed floor in EIP-7762 has focused on whether it is sufficiently low to account for potential future ETH price appreciation. The computer scientist in me would like to remark that this is a bit like trying to predict the appropriate cost of 128 kB of storage 50 years into the future based on the ability of the dollar to retain its value. It can be assumed that the cost of a fixed amount of data availability will fall drastically over the next half-century, both due to improvements in hardware and software, while Ethereum’s income from data availability still rises. Thus, we cannot ascertain the appropriate minimum price for one 128 kB blob based on ETH price considerations, but should instead codify the economic relationship between blob gas and execution gas, allowing the minimum price to adapt with future scaling. To be fair, the change in blob count might take place during a hard fork, and developers could then readjust the EIP-7762 threshold. But as argued, this is undesirable “tinkering”, and changes in blob count migh also happen automatically in the future.

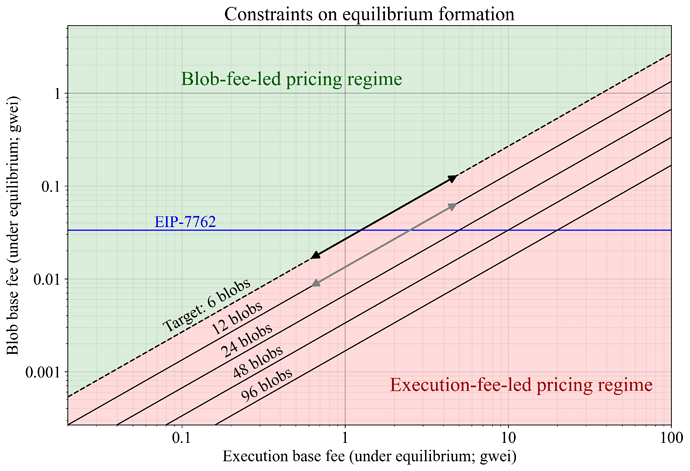
Figure 1 shows how the blob base fee floor adapts with the execution base fee in EIP-7918, while remaining fixed in EIP-7762. The price floor in EIP-7918 varies along the fee parity line, as indicated by arrows. When the target is 6 blobs, the floor has a higher baseline (black arrows) than when the target is 12 blobs (grey arrows), reflecting different opportunities to amortize execution costs across consumed blobs.

Figure 1. Comparison between EIP-7762 and EIP-7918. EIP-7762 stipulates a fixed threshold at 2**25wei. EIP-7918 stipulates a fee-parity threshold that varies with the execution base fee (the cost of the blob-carrying transaction) and the blob target (the opportunity to amortize the blob-carrying transaction).

Concerning implementation complexity:

• EIP-7762 changes one constant and adds block_timestamp as an input variable to calc_excess_blob_gas(). This input is included in an if statement evaluating timestamps, returning 0 if TRUE.
• EIP-7918 adds one if statement to calc_excess_blob_gas() evaluating computed gas prices, altering the return to be parent.excess_blob_gas + parent.blob_gas_used // 3 if TRUE.

Whether one change brings more complexity than the other is hard for me to tell. They should both be fairly similar and both be straightforward.

Question 4: Request for empirical analysis

@dataalways

I’m curious to the historical empirical impact of this proposal. How often would it have been a major contributor v.s. being overshadowed by blob fees?

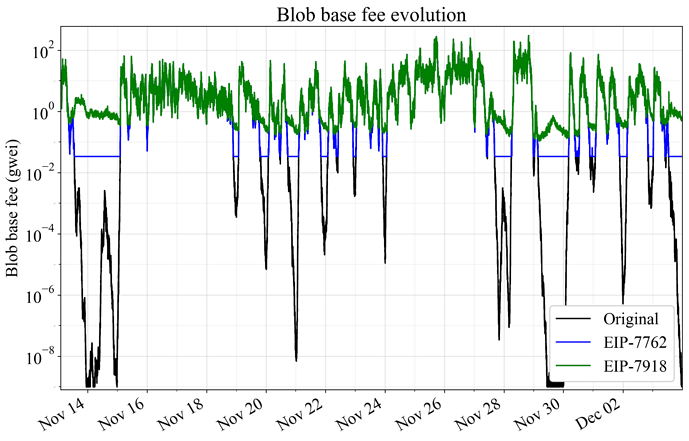
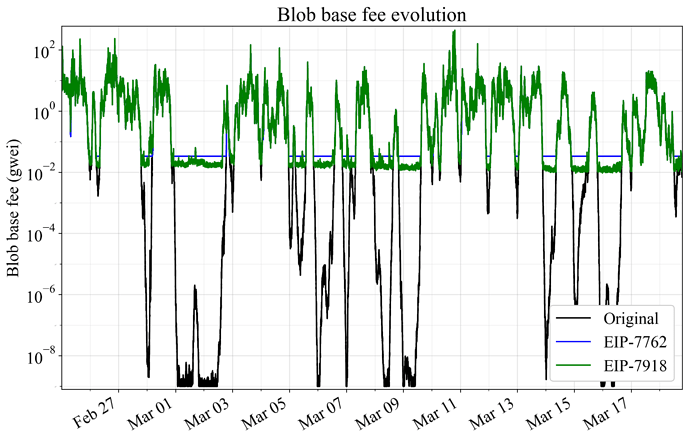
Figures 2-3 show price evolution over three weeks in November 2024, when the average execution base fee was around 16 gwei, as well as in March 2025, when the average was around 1.3 gwei. Thresholding of EIP-7762 (blue) and EIP-7918 (green) is applied directly to the original data, without accounting for its potential effect on the equilibrium fee. The equilibrium blob base fee would in reality rise from the threshold level once demand at this fee is above target supply. A target of 6 blobs was used as the amortization factor to make the comparison applicable to Pectra settings. As evident and in line with the previous Figure 1, the floor in EIP-7918 becomes higher than the floor in EIP-7762 when execution gas is more expensive, and lower when execution gas is cheaper.

Figure 2. Blob base fee evolution with the current fee market (black), with EIP-7762 (blue), and with EIP-7918 (green), during three weeks of November 2024 when the average execution base fee was around 16 gwei. Thresholding is applied directly to the original data, without accounting for its effect on the equilibrium fee.

Figure 3. Blob base fee evolution with the current fee market (black), with EIP-7762 (blue), and with EIP-7918 (green), during three weeks of March 2025 when the average execution base fee was around 1.3 gwei. Thresholding is applied directly to the original data, without accounting for its effect on the equilibrium fee.

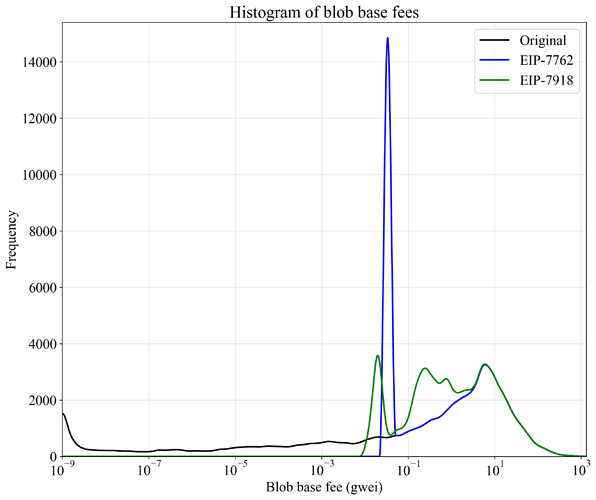
Figure 4 shows histograms for the four-month period from the start of Figure 2 to the end of Figure 3, corresponding to approximately 900k blocks beginning at block number 22075724. The histograms employ 100 log-spaced bins per decade (factor-of-ten increase), which are smoothed using a Hanning window of width 41 with mirror-reflected edges. The threshold set by EIP-7918 (green) can operate both below or above the threshold set by EIP-7762 (blue), depending on the cost of execution gas.

Figure 4. Histogram of the blob base fee when applying EIP-7762 (blue) or EIP-7918 (green), with light smoothing applied. A four-month period from November 2024 through March 2025 was analyzed. Thresholding is applied directly to the original data, without accounting for its effect on the equilibrium fee.