I will in this answer try to explain what adapting with scaling means and why it is necessary for a blob base fee threshold. First to briefly answer the question more directly: the if-clause depends on both execution costs and the targeted number of blobs. Therefore, if more blobs are targeted, the execution base fee must be higher to have an effect on the blob base fee.
There are essentially two different axes by which blob base fee thresholds can adapt: with the execution base fee and with blob quantity. This leads to a quadrant in scaling adaptation strategies, as outlined in Table 1.
| Scaling adaptation paradigms | ||
|---|---|---|
| Quantity↓ Execution→ | No | Yes |
| No | EIP-7762 | EIP-7918E |
| Yes | EIP-7918Q | Full EIP-7918 (EQ) |
Table 1. The scaling quadrant for blob fee thresholds. Full EIP-7918 adapts with both blob quantity and execution base fee, and EIP-7762 adapts with neither. Versions of EIP-7918 that only scale with execution base fee (E) or blob quantity (Q) are also reasonable to consider.
In general terms, the if-clause for an EIP-7918Q implementation looks like this:
if AGGREGATED_BLOB_BASE_FEE_THRESHOLD > BLOB_QUANTITY * get_base_fee_per_blob_gas(parent):
In this scenario, BLOB_QUANTITY can derive from the target number of blobs, and the AGGREGATED_BLOB_BASE_FEE_THRESHOLD will apply to an aggregation of the blob base fee over some stipulated blob quantity. The floor can be fixed to AGGREGATED_BLOB_BASE_FEE_THRESHOLD when the if-clause returns TRUE.
The if-clause for an EIP-7918E implementation looks like this
if TX_COST * parent.base_fee_per_gas > GAS_PER_BLOB * get_base_fee_per_blob_gas(parent):
When this if-clause returns TRUE, the blob base fee should rise smoothly according to:
return parent.excess_blob_gas + parent.blob_gas_used // 3
as in the original implementation. An EIP-7918E implementation was previously suggested by Ben Adams, relying on POINT_EVALUATION_PRECOMPILE_GAS to establish a neutral threshold.
Two reasons for adapting with blob quantity can be outlined:
- Q1 – As DA scales, blob consumers can scale up consumption, allowing them to amortize their fixed execution costs (e.g., proof verification for ZK rollups, and batch posting costs for optimistic rollups) across more posted blob data.
- Q2 – As DA scales, the upper end of the possible long-run ETH-denominated price per blob will fall.
The first reason (Q1) has been the main focus previously. As the targeted number of blobs increases, the fixed costs fall relative to the variable costs, and the blob fee market (which covers the variable costs) can then remain functional under a lower blob base fee, still influencing the quantity of blobs demanded. The second point (Q2) is however also important: as the quantity of blobs per block increases, the upper end of the long-run average income that Ethereum can expect to derive from each blob should fall.
First of all, technological progress generally brings down the unit cost of data services, as observed in many areas following Nielsen’s law and Moore’s law.
In the case of Ethereum’s DA services, there is also a specific reflexivity that is important to understand and that will now be explored further. Aggregate ETH-denominated income from DA affects the fiat-denominated value of the ETH token, reflexively bounding the possible long-run ETH-denominated income, thus bounding the per-unit price of blobs.
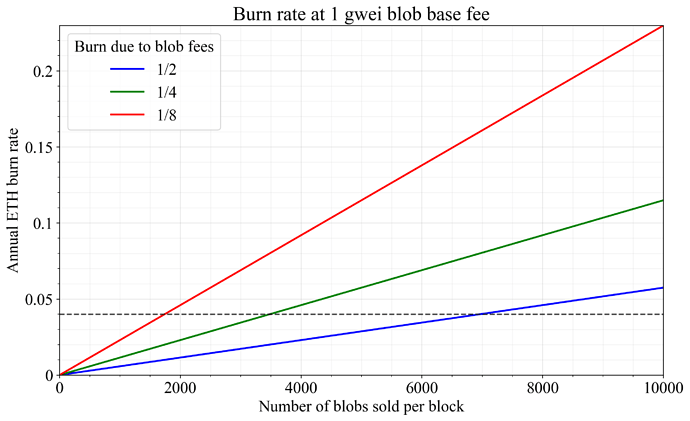
As an example, assume that technological progress allows Ethereum to scale both the execution layer and DA, with a target of 4000 blobs 10 hard forks from now. Further assume that 1/4 of Ethereum’s income (focusing here on burned ETH and ignoring MEV) derives from DA and 3/4 from the regular execution gas burn, and that there is a minimum blob base fee of 1 gwei. In this scenario, the burn rate would be a whopping 4.6%. The long-run burn rate cannot be too high for a PoS chain with a low issuance rate such as Ethereum, given a reasonable monetary premium and a “tech premium”. The token becomes too valuable to hold when accounting for “token buybacks”, use as money, and future prospects, and the price of ETH must rise, thus pushing the burn rate back down as the fiat-denominated cost facing the consumer becomes prohibitive. Figure 1 illustrates the relationship between the number of blobs per block sold at a 1 gwei blob base fee and the burn rate, with the burn rate specifically derived from blob base fees at various proportions.
Figure 1. Relationship between the number of blobs per block sold at a 1 gwei blob base fee and the burn rate.
A burn rate of 4% is illustrated by a dashed line in the figure, corresponding to a ratio between market cap and annualized burn of 25. A fixed threshold such as 1 gwei explored in the figure would undeniably put a ceiling on the number of blobs that can be consumed on average in the long run. The threshold then effectively act as a cap on blob quantity, regardless of the specified target.
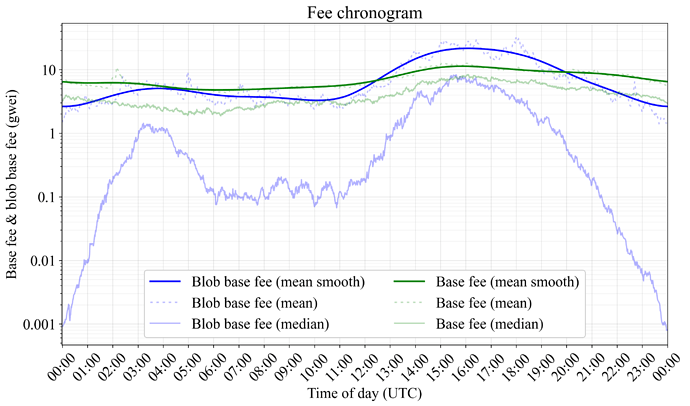
Such a threshold would however have detrimental effects at far lower blob targets. Figure 2 shows how the price of blob gas and execution gas varies across the day in a chronogram. During the overlap in business hours between Western Europe and the U.S., the gas price is on average the highest. The mean smoothed blob base fee varies by almost an order of magnitude (10x) across the day, and the median varies by around four orders of magnitude (10000x). Variation between different days is also substantial. Any threshold will particularly affect parts of the world doing business during a time in the day differing from Western Europe and the U.S. From a fairness perspective, it is therefore important to have a clear rationale for the threshold level, for example preserving a functioning fee market. Accounting for the execution costs when setting the threshold arguably also directly improves fairness: the threshold will then on average be lower outside of EU/U.S. business hours, since execution base fees (green line in Figure 1) naturally covaries with the blob base fees (blue line). It is also important from a fairness perspective to make the threshold adaptive, taking away the need for developers to re-adjust it as Ethereum scales.
Figure 2. Fee chronogram illustrating how fees vary over the day.
When it comes to adapting with the execution costs, this is what allows (Q1) to be fully modeled. One hypothetical rationale for adapting only with execution costs and not with blob quantity is that execution gas limits and blob gas targets could evolve roughly in the same direction, such that the associated fall in the base fee for both matches. Full EIP-7918 can navigate such assumptions in two ways, either by in that scenario slowly subsiding (while still remaining relevant for several decades) as the fee market starts functioning better, or by imposing sub-linear adaptation strategies.
In conclusion, a fixed threshold would need to be re-adjusted by developers as Ethereum scales, at least if scaling is substantial. This sort of re-adjustment should be avoided. A particular strength of cryptoeconomics is the ability to encode promises that extend into the future, and EIP-7918 allows for this, by automatically adapting the threshold.