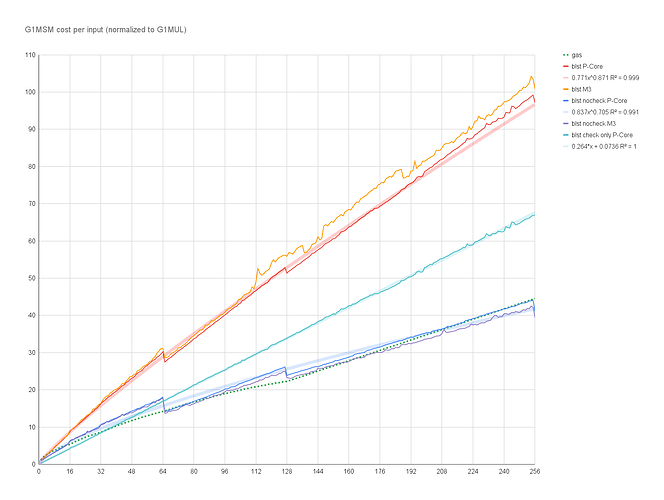
BLS precompile g1msm gas cost analysis
We’ve implemented EIP-2537: Precompile for BLS12-381 curve operations in evmone using blst v0.3.13 library. Then, we’ve benchmark multi-scalar multiplication g1msm in this implementation and compared timings with the specified gas schedule.
Benchmarks have been done on 2 different CPU architectures:
- x86-64 Intel Ultra 7 155U Performance Core 4.0GHz
- arm64 Apple M3 Pro
Timings have been normalized to single point multiplication (precompile g1mul). I.e. single naive multiplication is 1.
We also benchmark variant of g1msm with subgroup checks disabled (“nocheck”).
The chart also includes the line “gas” of by-the-spec gas cost. It is “discounted” up to 128, then linear with slope 174/1000.
Finally, we’ve added the “check only” line which is difference between default and “nocheck” series.
Conclusions
The real cost of the precompile is close to linear with slope 100/256 and is significantly higher than the estimated by the gas cost. While, the cost of the precompile without subgroup checks is sub-linear and “relatively” matches the gas cost.
In order to approximate the cost of the subgroup check component of the operation, we analyze the difference of time taken by the “check” and “nocheck” variant. It is visible from the chart that slope of the data is constant for various $n$ (contrary to that of the “check” and “nocheck” slopes which gradually decrease). So we have a sub-linear (piecewise linear) component of the MS itself and a linear component of the subgroup check, which aligns with the theoretical expectations
In other words, the g1msm precompile is compound of linear and sub-linear operations, therefore it total complexity is linear.
The gas schedule, specifically the discount table, was proposed in the initial commit BLS12-381 curve operations from 2020 and hadn’t been updated since.
The subgroup check was added two years later in 2022 by the Update EIP-2537: Rephrased subgroup check part.
We should get under consideration once again if the subgroup check is needed for point multiplication. The algorithms (mul and msm) works well on every point from the curve. This check seems to be added only because of not very clear security consideration. Moreover, making this check for every call is unnecessary when the programmer is sure that the input is in proper subgroup. I.e it’s a result of previous operation which does not change the subgroup.