I finished fully implemented EIP-2537 in Constantine in EIP-2537 - BLS12-381 precompiles for the EVM by mratsim · Pull Request #368 · mratsim/constantine · GitHub and now can provide accurate benchmarks that take into account (de)serialization and other miscellaneous costs.
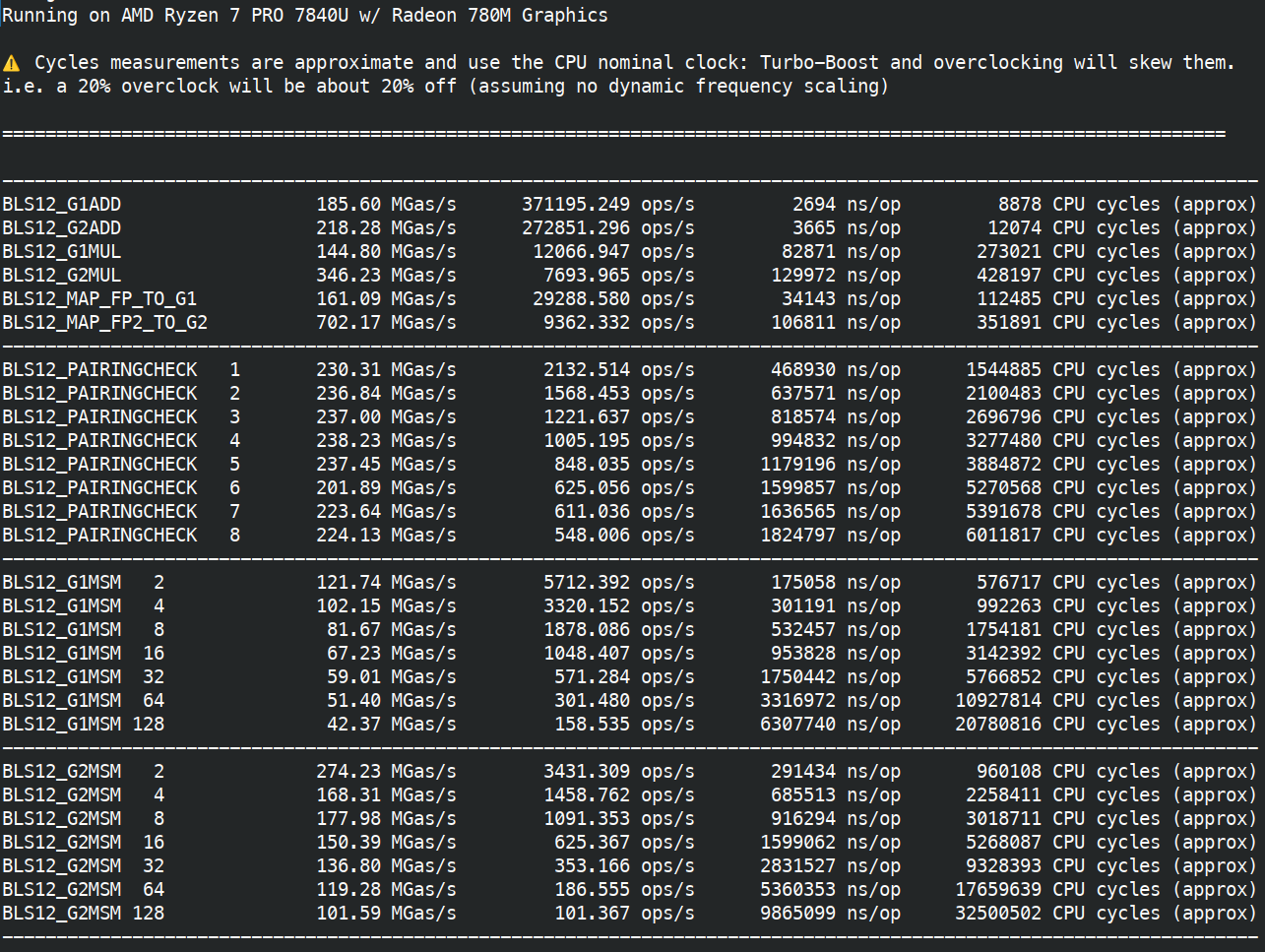
First on AMD Ryzen 7840U (2023, low power / ultraportable version of their flagship 7840U, TDP 28W down to 15W, 3.3GHz turbo 5.1GHz) with assembly and Clang.
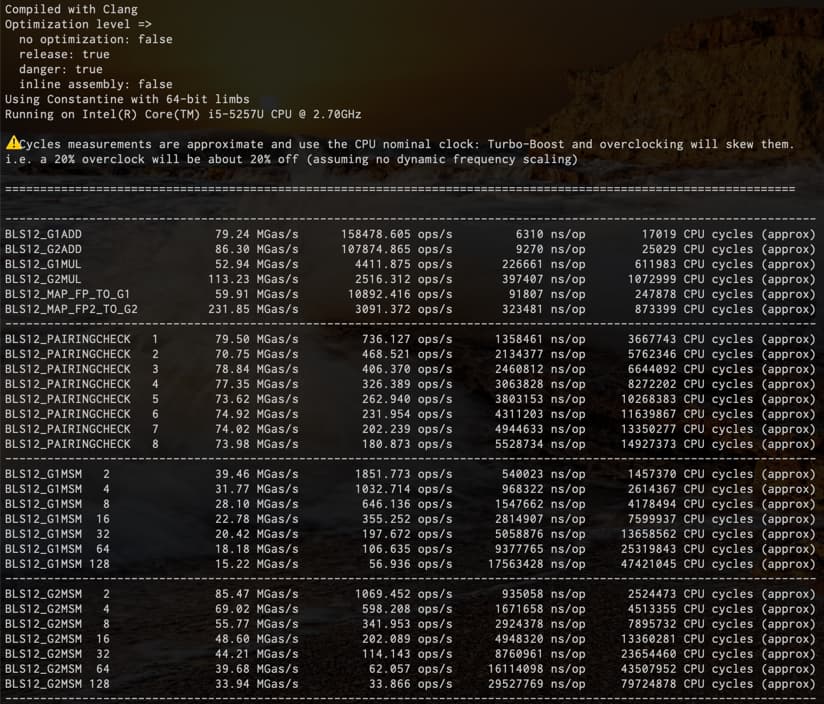
Second on i5-5257U (Macbook Pro 2015, low power dual core Broadwell, TDP 15W down to 7.5W, 2.3GHz turbo 2.9GHz) without assembly (it doesn’t have ADOX/ADCX instructions as well), but we do use the add-with-carry intrinsics. This is a 9 year old x86 CPU.
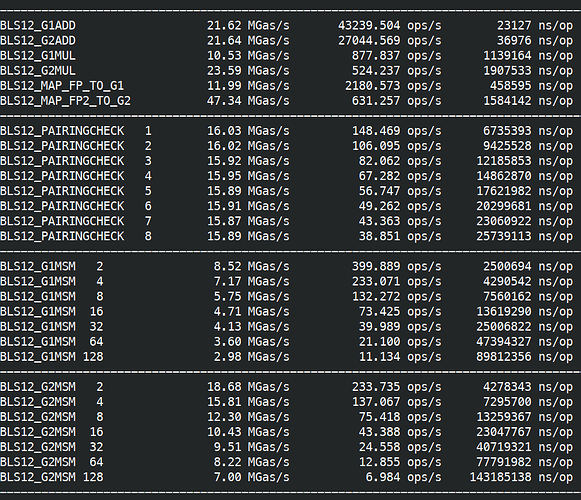
Finally on a Raspberry Pi 4 (2019, TDP 10W, 1.5GHz) without assembly, and without any add-with-carry intrinsics. No add-with-carry makes bigint operations up to 3x more costly has add-with-carry need to be replaced by main addition, comparison/carry check, adding the carry.
See also compiler codegen Compiler Explorer and Tracking compiler inefficiencies · Issue #357 · mratsim/constantine · GitHub
Price suggestions
This remark is confirmed with end-to-end test.
Besides MSMs all operations can achieve 60Mgas/s on a 9 year old very low-powered CPU (15W!), without assembly. and even 230Mgas/s for mapping to G2. This strongly suggests that those operations are overcosted.
I think that 9 year old, 15W CPU is significantly outdated and achieving 20Mgas/s without assembly on it should be fine.
Hence I suggest the following price changes:
| Primitive | Current price | Suggested price | Ryzen 7840U 28W 3.3GHz turbo 5.1GHz - clang+ASM - current | Ryzen 7840U 28W 3.3GHz turbo 5.1GHz - clang+ASM - repriced | Intel i5-5257U 15W 2.3GHz turbo 2.8GHz - clang+noASM+intrinsics - current | Intel i5-5257U 15W 2.3GHz turbo 2.8GHz - clang+noASM+intrinsics - repriced |
|---|---|---|---|---|---|---|
| BLS12_G1ADD | 500 | 125 | 185.60 MGas/s | 46.4 | 79.24 MGas/s | 19.81 |
| BLS12_G1MUL | 12000 | 3800 | 144.80 MGas/s | 45.9 | 52.94 MGas/s | 16.8 |
| BLS12_G2ADD | 800 | 170 | 218.28 MGas/s | 46.325 | 86.30 MGas/s | 18.33 |
| BLS12_G2MUL | 45000 | 6100 | 346.23 MGas/s | 46.9 | 113.23 MGas/s | 15.35 |
| BLS12_MAP_FP_TO_G1 | 5500 | 1600 | 161.09 MGas/s | 46.86 | 59.91 MGas/s | 17.43 |
| BLS12_MAP_FP2_TO_G2 | 75000 | 5000 | 702.17 MGas/s | 46.8 | 231.85 MGas/s | 15.46 |
The rationale for those changes is targeting a CPU 2~3 years older than my own for 30Mgas/s, CPUs are progressing on average by 10~15%/year, something that is 66% perf is reasonable (so around 45Mgas/s). But that said that CPU is still a low-power CPU, so instead of targeting 45Mgas on it we can target 40Mgas or even 35Mgas.
In any case it is clear that G2 functions are severely overcosted, especially mapping to G2.
Pairings
For pairings, the evolution of cost for multipairing is stable but the price is 5x the actual cost.
Hence I suggest moving from 43000*k + 65000 to 8600*k + 13000
MSMs
The discounts are too steep and need adjustment.
| Primitive | Current cost | Suggested cost | Ryzen 7840U 28W 3.3GHz turbo 5.1GHz - clang+ASM - current | Ryzen 7840U 28W 3.3GHz turbo 5.1GHz - clang+ASM - repriced | Intel i5-5257U 15W 2.3GHz turbo 2.8GHz - clang+noASM+intrinsics - current | Intel i5-5257U 15W 2.3GHz turbo 2.8GHz - clang+noASM+intrinsics - repriced |
|---|---|---|---|---|---|---|
| G1MSM 2 | 2 * 12000 * 888 / 1000 = 21312 | 2 * 3800 * 999 / 1000 = 7592 | 121.74 Mgas/s | 43.37 Mgas/s | 39.46 Mgas/s | 14.06 Mgas/s |
| G1MSM 4 | 4 * 12000 * 641 / 1000 = 30768 | 4 * 3800 * 919 / 1000 = 13969 | 102.15 Mgas/s | 46.38 Mgas/s | 31.77 Mgas/s | 14.42 Mgas/s |
| G1MSM 8 | 8 * 12000 * 453 / 1000 = 43488 | 8 * 3800 * 813 / 1000 = 24715 | 81.67 Mgas/s | 46.41 Mgas/s | 28.10 Mgas/s | 15.97 Mgas/s |
| G1MSM 16 | 16 * 12000 * 334 / 1000 = 64128 | 16 * 3800 * 728 / 1000 = 44262 | 67.23 Mgas/s | 46.40 Mgas/s | 22.78 Mgas/s | 15.72 Mgas/s |
| G1MSM 32 | 32 * 12000 * 268 / 1000 = 102912 | 32 * 3800 * 668 / 1000 = 81229 | 59.01 Mgas/s | 46.58 Mgas/s | 20.42 Mgas/s | 16.12 Mgas/s |
| G1MSM 64 | 64 * 12000 * 221 / 1000 = 169728 | 64 * 3800 * 630 / 1000 = 153216 | 51.40 Mgas/s | 46.40 Mgas/s | 18.18 Mgas/s | 16.41 Mgas/s |
| G1MSM 128 | 128 * 12000 * 174 / 1000 = 267264 | 128 * 3800 * 602 / 1000 = 292813 | 42.37 Mgas/s | 46.42 Mgas/s | 15.22 Mgas/s | 16.65 Mgas/s |
| G2MSM 2 | 2 * 45000 * 888 / 1000 = 79920 | 2 * 6100 * 999 / 1000 = 12188 | 274.23 Mgas/s | 41.82 Mgas/s | 85.47 Mgas/s | 13.03 Mgas/s |
| G2MSM 4 | 4 * 45000 * 641 / 1000 = 115380 | 4 * 6100 * 919 / 1000 = 22424 | 168.31 Mgas/s | 32.71 Mgas/s | 69.02 Mgas/s | 13.41 Mgas/s |
| G2MSM 8 | 8 * 45000 * 453 / 1000 = 163080 | 8 * 6100 * 813 / 1000 = 39674 | 177.98 Mgas/s | 42.77 Mgas/s | 55.77 Mgas/s | 13.57 Mgas/s |
| G2MSM 16 | 16 * 45000 * 334 / 1000 = 240480 | 16 * 6100 * 728 / 1000 = 71053 | 150.39 Mgas/s | 44.43 Mgas/s | 48.60 Mgas/s | 14.36 Mgas/s |
| G2MSM 32 | 32 * 45000 * 268 / 1000 = 385920 | 32 * 6100 * 668 / 1000 = 130394 | 136.80 Mgas/s | 46.22 Mgas/s | 44.21 Mgas/s | 14.94 Mgas/s |
| G2MSM 64 | 64 * 45000 * 221 / 1000 = 636480 | 64 * 6100 * 630 / 1000 = 245952 | 119.28 Mgas/s | 46.09 Mgas/s | 39.68 Mgas/s | 15.33 Mgas/s |
| G2MSM 128 | 128 * 45000 * 174 / 1000 = 1002240 | 128 * 6100 * 602 / 1000 = 470042 | 101.59 Mgas/s | 47.64 Mgas/s | 33.94 Mgas/s | 15.92 Mgas/s |
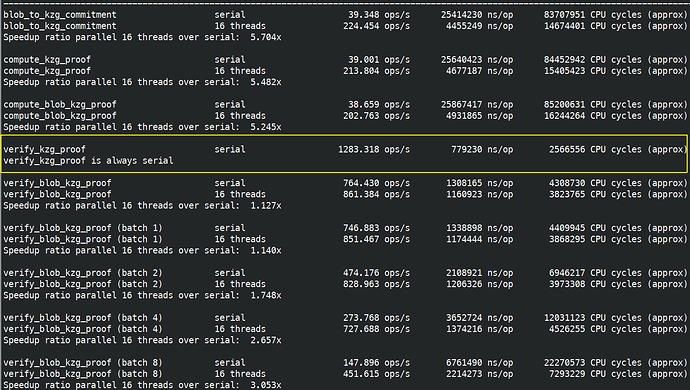
Comparison with EIP-4844 KZG
EIP-4844 introduced a point evaluation precompile that is mostly a double pairing at 50000 gas: EIP-4844: Shard Blob Transactions
On my machine that is 1283.318 operations/s so 64.17Mgas/s
Comparison with EIP-196 and EIP-197
- BN254 ECADD is at 500
- BN254 ECMUL is at 40000
- BN254 PAIRING is at 80000*k + 100000
I can introduce benchmarks later but they seem mispriced by a factor over 10x for multiplication and about 10x for pairings.