I’ll split my reply into an analysis and factual part and then my own opinion piece, then open up on something related to EIP-7667 on gas cost.
Analysis
I see 3 different paths:
- No change approach. no subgroup check, price like double-and-add and Pippenger today and add test vectors. For MSMs, in both Gnark and Constantine, endomorphism acceleration was not a problem or was even slower due to probably decomposition overhead + memory bandwidth / hardware cache limitations (at least on x86, Apple memory likely behaves differently).
- Misuse resistance approach. See @asanso, enforce subgroup check except on addition.
- Modular approach or performance approach, provide subgroup_check and clear_cofactor as separate primitives. People can cache subgroup_checks and ensure their cost is only paid once. Issue: they need to learn what a subgroup and cofactor is.
Now, for a more informed decision, we’re okay with the pricing of regular scalar-multiplication as double-and-add, but is endomorphism acceleration important for MSM?
When optimizing for G1, on my machines beyond 2^10 points (1024), endomorphisms were slower and so are deactivated: constantine/constantine/math/elliptic/ec_multi_scalar_mul.nim at 976c8bb215a3f0b21ce3d05f894eb506072a6285 · mratsim/constantine · GitHub
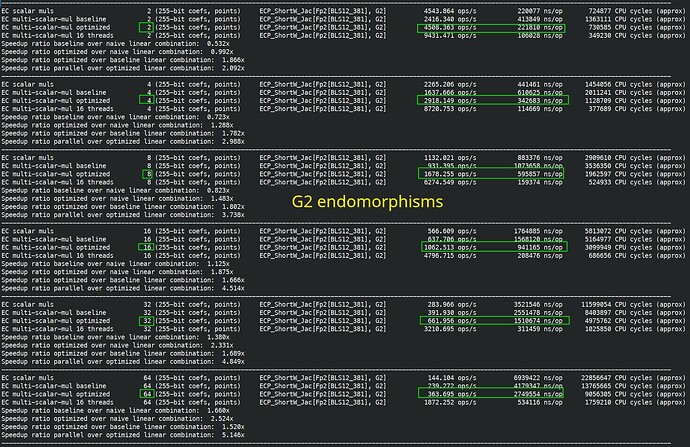
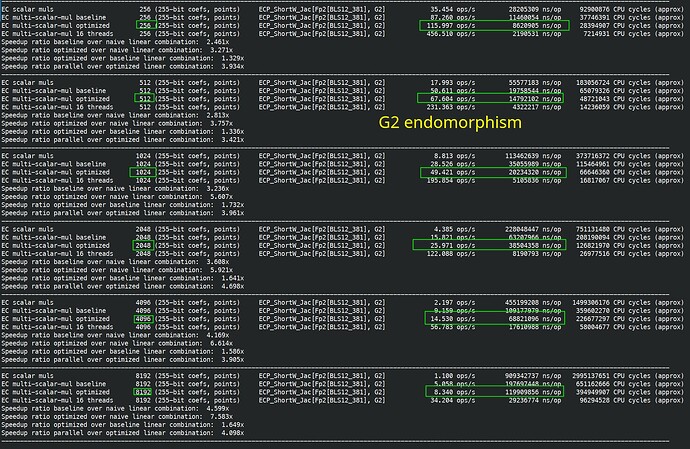
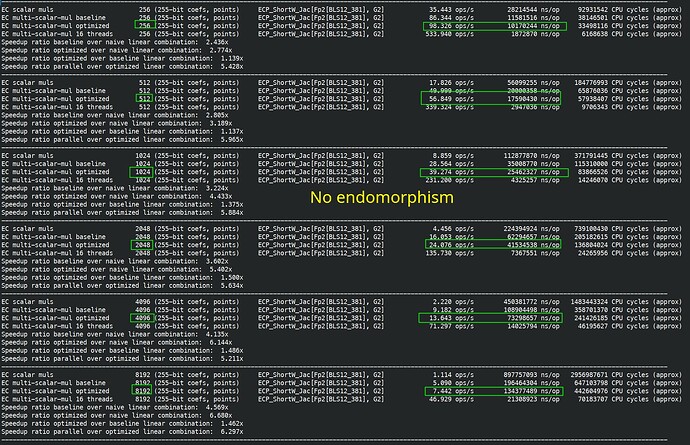
One extra remark is that on G1, endomorphism cut the scalar size from 255 bits to 128 bits. On G2, you cut the scalar size from 255 bit to 64 bit, further benchmarks confirm that similarly, there is a threshold, where endomorphism acceleration doesn’t really help.
With endomorphism:
No endomorphism:
Opinion
1 If not properly tested, the “no change” approach is likely to lead to state split if people start using point on curve but not in subgroup. If properly tested, the only difficulty is if some libraries do not allow selection of scalar multiplication algorithm and use endomorphism by default.
3 is similar to 1 in the happy path. In the unhappy path, will users respect a “Before calling the scalar-mul precompile, input MUST be subgroup-checked or coming from clear_cofactor or mapping_to_curve)”? If not, libraries can’t use the endomorphism accelerated path and we might as well use 1.
2 sounds like the reasonable choice.
Source code: constantine/constantine/math/elliptic/ec_multi_scalar_mul.nim at 976c8bb215a3f0b21ce3d05f894eb506072a6285 · mratsim/constantine · GitHub
Now for pricing the subgroup checks, I’ll use Scott, https://eprint.iacr.org/2021/1130.pdf, but there is a later note from El Housni:
- G1: P is in the 𝔾1 subgroup iff ϕ(P) == -u², ϕ is cubic root of unity endomorphism and costs 1 fp_mul, u is the curve parameter and is 64-bit with low hamming weight, hence about ~130 fp_muls for subgroup checks. A 255-bit double-and-add is on average 255+127.5 fp_mul so the ratio subgroup_check/scalar_mul is about 1/3.
- G2: P is in the 𝔾2 subgroup iff ψ(P) == u ψ is Frobenius endomorphism and costs 1 fp2_mul, u is the curve parameter and is 64-bit with low hamming weight, hence about ~70 fp2_muls for subgroup checks. A 255-bit double-and-add is on average 255+127.5 fp_mul so the ratio is about 1/5.
El Housni latest paper on subgroup checks:
- On subgroup checks for BLS12 - HackMD
- https://eprint.iacr.org/2022/352.pdf
- https://members.loria.fr/AGuillevic/files/talks/22-Aarhus-Crypto-Day.pdf
Gas costs
Better discussed here probably: EIP-7667: Raise gas costs of hash functions - #6 by mratsim
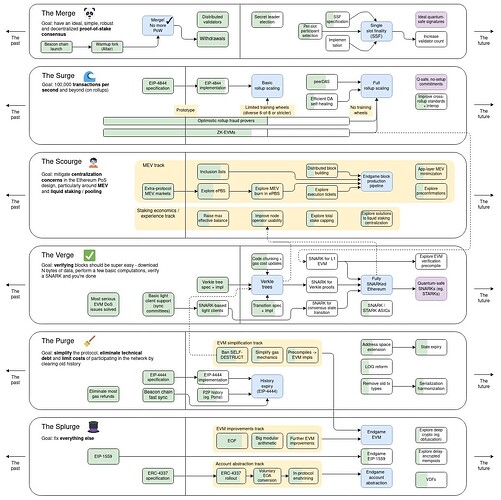
but here is the gist, some operations are very expensive in zkEVMs and zkVMs like hash functions, and the Verge roadmap endgame is having a snarkified EVM (text: Annotated Ethereum Roadmap and https://twitter.com/VitalikButerin/status/1741190491578810445)
So EIP-7667 proposes to raise gas cost of hash functions. But should BN254 and BLS12-381 also reflect that?