Answered in Discord, but for continuity answering here as well:
Miners won’t accept transactions without a tip (at least not profit seeking rational ones that aren’t getting paid some other way).
My issue is just that it slows down the process. If you want to break EIP-1559 into smaller chunks, that’s great, but given the current political climate that seems like it would slow the deployment. I would be elated if I was proven wrong about this by someone else trying it out. 
Usually splitting things up into smaller more manageable chunks facilitates moving things through more quickly because people can focus their efforts on the pieces they care about, and you don’t end up with one contentious piece holding everything else up. Do you believe that isn’t the case for Ethereum hard fork inclusion stuff? If not, do you have any idea why that isn’t the case?
Just saw your comment @vbuterin
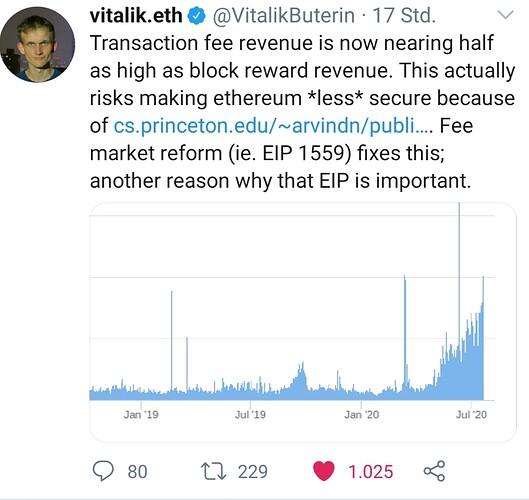
Could you lay out the thought how eip-1559 helps with the attack described in the paper? I was thinking about the impact myself but concluded that because the anticipated equilibrium in https://www.cs.princeton.edu/~arvindn/publications/mining_CCS.pdf has only half filled blocks it would keep the MINFEE at 0 and hence not change anything on the problem.
There was another paper proposing payout of the transaction fee in a sliding average window of the last 10 blocks. That might fix the risk of the petty miner scheme and could be quick follow of 1559.
I’ll let someone else give the more complete response, but the gist of it is that 1559 burns congestion-related fees, thus miners would not profit from reorgs for fees.
If MINFEE is 0 then the system either is broken or demand for using Ethereum is legitimately low (which we haven’t seen for quite a while and seems unlikely to happen soon). Equilibrium for 1559 is half full blocks, but under the assumption of raw demand for Ethereum block space being greater than supply of block space. It is the fee going above 0 that drives final demand down to equal with 50% of block space supply.
Yes problably broken is the right description or at least manipulated. I’m quoting from the mining_CCS.pdf paper, highlights by me:
Once any non-zero fraction of miners is PettyCompliant, it enables various strategies that are more aggressive and harmful to Bitcoin consensus. We call this the undercut-ting attack, where miners will actively fork the head of the chain and leave transactions unclaimed in the hope of incentivizing PettyCompliant miners to build on their block. In some scenarios, our simulation reveals a non-equilibrium with increasingly aggressive undercutting. But with an expanded strategy space, and suitable assumptions, we are able to prove that an equilibrium exists. However, it is one where miners include only a fraction of available transactions into their blocks. This results in a backlog of transactions whose size grows indefinitely with time. We confirm this result using simulation.
So when miners include only a fraction of available transactions into their blocks then my understanding is MINFEE would stay 0. It’s misbehavior, but misbehavior that might turn out to be more profitable to the miners.
This isn’t true. With 1559, MINFEE would be 0 only if a plurality of miners (exact portion changes depending on how much they sacrifice, but it can be as high as over 50%) all sacrifice profits in order to drive the fee down. As long as they do this, any miner that defects from this strategy will be more profitable than miners executing the attack as long as the attack continues. When the attack is no longer executed by a sufficient portion of miners, the base fee will rise back up to its correct level.
This means that any miner that defects from the attack is rewarded, and any miner that participates in the attack is punished for as long as the attack is ongoing. Also, we can adjust the portion necessary to successfully drive the base fee down by increasing the block size target. Current EIP specifies the target as being “half full” but we could just as easily target 1/4 full which would increase the hashing power required to attack the system in this way by ~2x. The only downside of that is that we end up with bigger block size spikes and it is unclear how various client implementations will handle that so we are starting with only a 2x block size spike being possible.
Something to keep in mind is that a 1559-like fee system is sufficiently different from the system the paper is attacking that the attack no longer makes sense. Because of this, outcomes from that paper cannot be applied to a 1559-like system directly. If you want to describe an attack against a 1559-like system, you will need to fully describe a new attack.
Imagine the situation “When X = 1 and Y = 2 then X+Y = 3”. If you change X to equal 5, the conclusions that X+Y=5 no longer holds and you will need to re-evaluate things. In this case, the paper is built on the premise that fees are allocated in a very specific way, and when you remove that premise the rest of the paper no longer falls out.
Note: It is certainly possible that an outcome like the one described in that paper is possible, but I believe it would need a pretty significant rework to draw that conclusion.
Maybe this would help killing this bad equilibrium
Can’t find the paper anymore but I read an idea about creating a FEEPOOL. All spend transaction fees would be added to the FEEPOOL, and a block miner would receive 1/8th of that FEEPOOL for a new block. The MINFEE would stay and guide users to pay more when there is congestion, while miners would be incentivized keep blocks filled so the FEEPOOL stays high and miners would be less worried about tricking the previous or next block for transactions as their fee based revenue is less spiky. In fact miners could be incentivized more since I think burning fees below MINFEE would not be needed in this case and could just be added to the FEEPOOL…
The paper is saying the opposite. Miners are incentivized to drive the fees up, but drive the MINFEE down, so that the tip maximizes. When a miner creates a filled block that has a higher MINFEE then that creates an incentive for all other miners to ignore this block as it reduces all future revenue from transactions. In fact the incentive to game the system gets bigger.
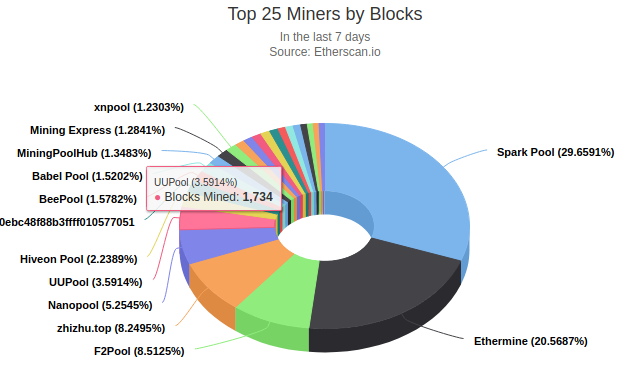
E.g. for Spark Pool and Ethermine each step higher MINFEE would mean to surrender future transaction profits on their 29% / 20% share of all blocks.
True, I was just curious which aspect of 1559 specifically is the part that is disabling the mentioned attack as twittered by Vitalik. For me it seems 1559 in it’s current form incentivizes the attack even more.
– We have posted nearly at the same time, so see my previous post for a patch proposal on EIP-1559 to remove the gaming incentive.
This has been discussed here in this thread I believe. I forget what the arguments against it are but I think it was just something like, “why miners instead of everyone?”
The paper wasn’t about 1559 either. ![]()
If a miner controls 51% of hashing power then they can do some pretty bad things to Ethereum, including simply ignoring all other miner blocks to maximize their block reward. 1559 doesn’t really change that in any meaningful way, and if someone wants to exploit 51% of hashing power for financial gains there are far more efficient ways to do so than driving the fee down. Something to keep in mind is that this sort of attack is collusion resistant because there is a financial incentive to defect, and you can defect anonymously. Because of this, it is very hard for miners to collude to execute the attack.
As far as mining pools go, keep in mind that any mining pool that is executing this attack will become less profitable than a mining pool that doesn’t execute the attack, which means pool participants can (and potentially will) individually defect if a mining pool is detected to be executing an attack like this.
It is the fee burning aspect that does it.
Thanks for the discussion @MicahZoltu , it’s good to keep the ball moving here. Very curious about the impact of EIP-1559 on the fee market once it’s deployed. If there are side-effects fixes such as FEEPOOL can still be discussed then.
Shall we set the denominator to 8 for the downward movement and 7 for the upward movement to make the rate of change the same in both directions?
I’m not opposed, though there is a desire to limit non-critical consensus changes to the specification that you’ll need to push past, which I suspect will require an argument as to why we should care other than “because symmetry feels good”. 
Blog post that hopefully can help dispel some fear over 51% attacks against EIP-1559: https://medium.com/@MicahZoltu/eip-1559-51-attacks-should-you-live-in-fear-d817be3759dc?sk=59773d28b15446bacd5e5112e350e000
@dominic one major part of EIP 1559 that mitigates the attack is the part where the fact that fees are burned makes it economically safe to retain some issuance, which pushes the chain away from the fee-dominated world that the article describes. Additionally, the fee burn makes transactions themselves less profitable to include, compounding this effect.
Partially filled blocks don’t necessarily cut the MINFEE to zero; that would require average blocks to be less than half full on average, even when there is a high tip/bribe to be earned from including more.
Maybe I’m too pessimistic here about peoples (and miners) intentions but the mining_CCS paper postulated an equilibrium with half filled blocks because that would be most profitable for miners. The paper assumes that miners are players in game theory sense and strive to optimize their revenue, eventually forming a let’s call it “gas OPEC”. Not by direct collusion but by behaving economically efficient.
It just seems to me that with EIP-1559 there are many mining strategies that perform economically better than to just fill the blocks. More than without EIP-1559. In fact because of the burning of EIP-1559 the revenue difference between “fill all blocks” and “keep the blocks 1/2” is amplified creating (missing mathematical proof) an even greater incentive to form the “gas OPEC”.
This seems to be more a social experiment than a technical. So I’m super curious to see what happens really aftet deployed. Just was confused quoting this paper as solved – while I read it as amplified by 1559
Cheers and thanks for all the work @MicahZoltu @vbuterin
The mining_CCS paper’s premise depends on fees going entirely to miners and there being no protocol level base fee. When you add these things, the attacks described in the paper no longer make sense because they are built on a premises that are no longer true. Further, if you try to reconstruct the same attack with these new premises you’ll find that the attack no longer works.
If you believe that there is still a valid attack vector I encourage you to draft up the attack proposal (describe what strategy each participant is following) and it can then be evaluated directly.
An “attack” is simple. I wouldn’t call it an attack though, it’s just a mining strategy
# Mining only most expensive tx but less than
# TARGET_GAS so that BASE_FEE goes down
SELECT * FROM TRANSACTIONS ORDER BY gas_price HAVING SUM(gas_used) < TARGET_GAS_USED
E.g. they mine exactly lower than TARGET_GAS, so the MIN_FEE can only go down, but they never have to mine empty blocks. If nobody plays their game they will have 50% less tx fees than anybody else, but the BASE_FEE will shoot up and eat most of the TX revenue anyway. So not much lost.
If on the other hand more miners use this rule, the BASE_FEE will converge to it’s minimum and TX_FEES will compete with BLOCK_REWARD exactly like today.
Mathematical I think it’s important to consider the ratio between the total block reward and the contribution of tx fees to it:
REWARD = BLOCK_REWARD + TX_FESS
In Block 10041942
REWARD = 2 ETH (Block) + 0.15 ETH (Fees)
TX_FEES = 7.5%
In Block 10641942
REWARD = 2 ETH (Block) + 2.2 ETH (Fees)
TX_FEES = 53%
Giving up 50% of 0.15 in TX_FEES in the short term to gain 2.2 ETH TX_FEES in the long term seems a pretty good deal.
So another strategy could be to target a certain reward % from TX fees by fixing the tip/bribe. This might have been suggested somewhere else:
# Mining only tx above a certain tip threshold
SELECT * FROM TRANSACTIONS ORDER BY gas_price WHERE gas_price - BASE_FEE > 100GWEI
In this different miners could be setting different tip levels, maybe based on their cost. But the effect would be the same as in strategy #1, the BASE_FEE would be damped until the minimum tip is reached. But where is that new equilibrium?
Anyway the strategies become much more interesting with EIP-1559 and there are many more that could be explored. So I’m super curious where it will settle. There is also a big mid-term social effect. E.g. once miners go from the current high tx fee rewards to the low expected rewards after EIP-1559 deployment with default configuration, how will they react when thinking about the “good old times” when you could make 2.2 ETH from tx fees alone. It seems unavoidable that miners will somehow mess with this logic to optimize their revenue.
The blocks mentioned:
https://etherscan.io/block/10641942
https://etherscan.io/block/10041942
This is the exact attack I describe in my blog post above. The only difference is that I find the math to be simpler if you have the attacker/coalition split their hashing power between “empty blocks” and “double full blocks”. However, the arguments are no different if you instead have the miner mine a bunch of undertarget blocks instead.
The summary is the same as in that article: There exist 51% attacks that are profitable for everyone who joins your attack. 51% attacks against 1559 (as described here and in the article) are non-profitable for any individual who joins the attack. It is always better to not participate in the attack and instead just encourage others attack (so you can benefit from the attack without having to pay the cost).
Consider a hypothetical automated market maker as a protocol-level price oracle for the trading pair GAS/ETH whose reserve of gas and ether after the n-th trade are g_n and f_n \times g_n, respectively. Moreover, let g_{n+1} = g_n + M/2 - w_n, that is, g += excess. It can be proved that, the limit of f_n as the initial reserve g_0 goes to infinity is given by:
- the Almgren-Chriss additive formula in the case of constant sum market maker,
- and your proposed exponential formula in the case of constant product market maker.
This observation immediately implies that both of these update rules (and any other one based on another constant function market maker) are path independet. Ironically, this is exactly why we have arrived at these formulas in the first place when attempting to solve a simple instance of path dependence attacks.