Agree. Also, see this comment from @mdalembert which explains the outcome of your concern+gas tokens:
1 Like
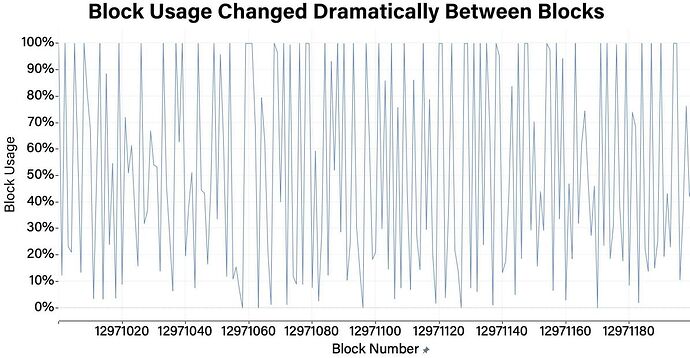
Interesting. Perhaps this is one of the reasons why gas tokens are being removed in London upgrade.
Since this is in Last Call and finalization is imminent, it would be useful to ensure the spec does not contain any TODOs. It seems these TODOs have nothing to do with 1559 itself, so suggest to remove them.
The current 1559 spec still has this in validate_block():
# TODO: verify account balances match block's account balances (via state root comparison) # TODO: validate the rest of the block
And the test cases section still only consists of TODO.
The TODOs in the python code are meant to indicate that around there is where a real client implementation would do those actions. They were never intended to be filled in in the specification as they are out of scope of this specification, but it is important to give context to readers as to how the changes described here integrate with a larger codebase. Iām open to other ideas on how to represent that.
I agree the test cases section should be removed.
Summary
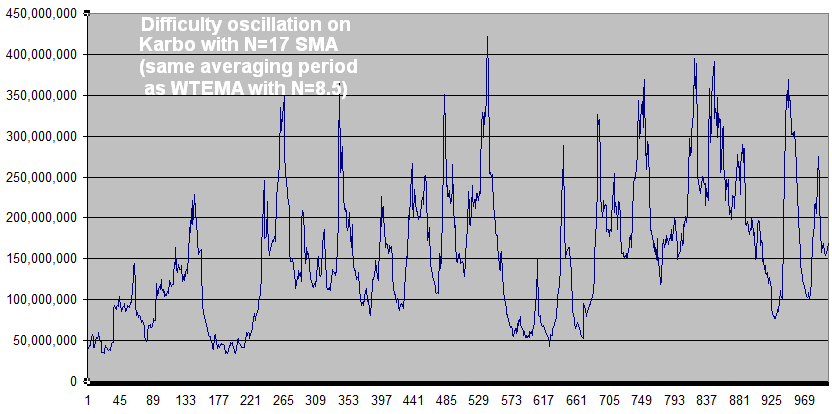
The large oscillations in the block fullness (see Coindeskās chart at bottom) was said in a Coindesk article to be caused by the new EIP-1559 base fee calculation. The goal is very much like the difficulty adjustment where the difficulty target has been replaced by the base fee and the solvetime is replaced by block fullness (both have a target they are trying to achieve). The EIP-1559 algorithm is the best possible for difficulty algorithms except for the very low setting seen in BASE_FEE_MAX_CHANGE_DENOMINATOR = 8. This would be pretty bad in difficulty algorithms due to resulting in similar oscillations (itās like a simple moving average using only the past 16 blocksā¦ see Karbo oscillations in next comment). It probably needs to be increased a lot. 30 would be a fast, tolerable difficulty algorithm and 100 to 500 would be a lot better. The 2000 that ETH uses for itās similarly-functioning DA is probably way too large. The base fee calculation has a strong parallel to difficulty algorithms, but itās hard to see how strong. Those paying fees are like miners on small coins who can come or go, amplifying oscillations. Itās not an exponential distribution, but the algorithm being used is durable for different distributions.
Details
The EIP-1559 code (see below) is called āWTEMAā by difficulty algorithm enthusiasts. Itās the same as ETHās difficulty algorithm but not as staccato, mathematically inverted (for the better), and uses an N=8 blocks instead of N=2000.
Hereās the simple math of EIP-1559, ignoring rounding error:
GF = base gas fee
F = block fullness in parent block as fraction of parent's target fullness
GF = parent_GF * (1 - 1/8 + F/8)
GF goes up as F increases above 1, so in difficulty algorithms, the parallel is that we replace GF with target (aka 2^256/difficulty) and F is parent_solvetime / target_solvetime.
Except for N=8 being really low, this is close to the best possible algorithm. If N=8 is substantially larger than F, itās equal to all of the following due to e^x = 1+x for small x where x = (F-1)/8
- 1st order IIR filter. See [1] for this and next 2
- Electronic RC filter (8-blocks) on how long it will take the error signal in the previous output sample to be applied on the same scale as the input signal.
- Kalman filter if the target value is a scalar random walk.
- Ideal EMA (exponential moving average) when applied to the exponential distribution of solvetimes in difficulty algorithms[3]. F=previous solvetime per target solvetime. GF = target = 2^256 / difficulty.
- BCHās new difficulty algorithm ASERT. (Lundeberg & Toomin, same result as above Imperial College paper)
You can use e^x =~ 1+x approximation to confirm itās equal to the following.
Ideal DA EMA / ASERT in "relative" form:
F = previous solvetime per target solvetime.
GF = target = 2^256 / difficulty.
GF = parent_GF * e^((F-1)/8)
In difficulty algorithms, N=8 is insanely low and causes these kind of oscillations.
F does not look like the same units as blocks which is what I interpreted the 8 to mean. To correct this serious problem (especially for the RC and difficulty algorithm parallels that are based on time), F can be interpreted as ānumber of blocksā to get ā1 target-blocks-worth of feesā.
EMA / ASERT are ideal for difficulty algorithms, but they have an exponential distribution. This seems to be important only in keeping it accurate for low N. This situation is probably not an exponential distribution so it may not be expected to work as well for low N, but for higher N, this algorithm is probably the best + simple that can be found.
EIP-1559 code:
elif parent_gas_used > parent_gas_target:
gas_used_delta = parent_gas_used - parent_gas_target
base_fee_per_gas_delta = max(parent_base_fee_per_gas * gas_used_delta // parent_gas_target // BASE_FEE_MAX_CHANGE_DENOMINATOR, 1)
expected_base_fee_per_gas = parent_base_fee_per_gas + base_fee_per_gas_delta
else:
gas_used_delta = parent_gas_target - parent_gas_used
base_fee_per_gas_delta = parent_base_fee_per_gas * gas_used_delta // parent_gas_target // BASE_FEE_MAX_CHANGE_DENOMINATOR
expected_base_fee_per_gas = parent_base_fee_per_gas - base_fee_per_gas_delta
From Coindesk article:
1 Like
Karbo coinās difficulty had oscillations very much like the current block fullness situation as a result of using an almost identical averaging period (aka āmean lifetimeā). N=16 block averaging in a simple moving average is the same āmean lifetimeā as EIP-1559ās EMA algo using N=8.
While Iām not opposed to changing the divisor, keep in mind that the primary goal (IMO) is user experience, which means strong guarantees that we donāt have many consecutive full blocks (because then people end up with stuck/pending transactions), and a secondary goal of minimizing the base fee change per block.
For a first attempt, Iām actually very happy with 8 because we see multiple full blocks in a row very rarely so far (though this may change as people switch to 1559 transactions), and 12.5% increase per block isnāt too high. We may be able to raise the denominator a bit without increasing the chances of many consecutive full blocks too significantly, but we need to be careful about breaking the primary target of ālow probability of consecutive full blocksā.
Also, I donāt think we should do much judging until end-users are widely using 1559 transactions. With most users using legacy transactions we should expect much higher rate of oscillation than if all users were using 1559 tranasctions.
Oscillations are a lot less efficient due to area under the curve being less for a given sum of the y values. Average base fee per block and average miner or staker bandwidth (computation and communication) requirements are (much?) higher due to the oscillations. Anyone needing to process and relay blocks ASAP (<1 second) has to have 2x the bandwidth for 1 or 2 blocks and then let the higher bandwidth sit idle for 2 or 3 blocks. Higher bandwidth requirements should cause higher gas prices, not just delayed txs.
The parallel between this and difficulty algorithms is strong. This seems more susceptible to oscillations because user can not only delay txs (like miners jumping from one alt coin to the next), but they also must come back at some point to send their txs (they donāt have an alternate coin to āmineā).
I spent a long time working on the difficulty oscillation problem in alt coins (see my github issues). The awful Karbo difficulty chart above with N=8 was my first algorithm. The solution was to make the averaging time very long, like N>100, and to remove any caps. Maybe there is a reason you canāt have blocks that are 10x bigger (or costly). In difficulty, the parallel would be a huge miner jumping on for ācheapā blocks. But they are not cheap because itās a fair, long-term āaverageā cost. Removing the cap isnāt as important as increasing āaveragingā window length, but it prevents the base fee from rising as fast as it should when thereās higher demand that the algo canāt see (due to the cap). The average block size (or computation gas) should be as easy to target and achieve as the average solvetime in difficulty algorithms.
Software might be developed to competitively exploit low fees. Itās a zero sum game, except if everyone uses the best software, no will get lower fees than others and it will reduce the oscillations (giving higher efficiency due to efficient competition). The net effect is if EIP-1559 had used a longer averaging window.
Since value is burned, the longest POW chain is not the sum of difficulties, but the sum of:
difficulty * (1+ base_fees/reward)
If this isnāt adjusted for, security is reduced (at least from what it could be).
Those willing to wait for txs to go through should have a lower base fee in exchange for waiting longer. EIP-1559 seems to try to assist in that goal. Hereās an idea to do it that builds on EIP-1559. Assign 1/4 the desired avg gas per block (avgGPB) to 889 out of every 1000 blocks and allow every 10th, 100th, and 1000th block to have gas per block targets of 10/4, 100/4, and 1000/4 times avgGPB. I donāt know if motivating 250x the normal gas every 1000th block like this is OK. Each of the 4 tranches has an independent base fee per gas calculation using the current formula which is,
BF = prior_BF * (1 - 1/8 + F/8)
but based only on their particular trancheās parent blockās F = āfullness fractionā:
F = tranche_parent_block_gas / tranche_gas_target.
tranche_gas_target = avgGPB * traunch / 4
traunch = 1, 10, 100, 1000.
A much better and complicated way is to equally share total base fees in the tranches instead of equally sharing total gas (over their respective intervals). It would greatly lower the really high tranche_gas_targets constant above by making it a variable. I havenāt worked out how to do it.
I said oscillations are inefficient because they require a higher bandwidth to āstop and goā. In other words, the average bandwidth required of the nodes (if they have to get the block out ASAP) is higher for a given amount of gas āper 100 blocksā if the bandwidth (gas per block) is changing up and down. But having the slower-tranche txs available ahead of time allows the bandwidth to be spread out, i.e. the bytes can be propagated and validated ahead of time.
Although intended as a relatively straightforward upgrade to Ethereumās fee mechanism, EIP-1559 has taken a life of its own in the form of the popular āultrasound moneyā meme that emphasizes the burning of base fees. While āThe Burnā is a positive byproduct of EIP-1559ās design, making Ether deflationary was never the intended goal of burning base fees (even if narratives post-2019 have reinforced this idea).
The misunderstanding about EIP-1559ās true design goals has affected the quality of discourse around Ethereumās monetary design, necessitating a reevaluation of EIP-1559 and a discussion of the issues that led to the communityās adoption of the proposal. This report from 2077 Research explains EIP-1559 from first principles and demonstrates the importance of a mechanism for efficiently allocating a scarce resource like blockspace on Ethereum: EIP-1559: Separating Mechanisms From Memes.
The report is geared at āseparating mechanisms from memesā and discusses the details of the EIP-1559 transaction fee mechanism (TFM). We also compare the experience of users under the legacy transaction fee mechanism to the experience of transacting post-EIP1559, demonstrating improvements in transaction UX.
By outlining the practical benefits dynamically adjusted base fees for the Ethereum network, we hope to correct the widespread misconception around EIP-1559 and make it clear that improves the efficiency of allocating scarce blockspaceānot an effort to āaccrue valueā by any means. We also hope this report will lead to better appreciation of EIP-1559, particularly as newer blockchains continue to face issues partially or wholly mitigated by the fee market design.
1 Like